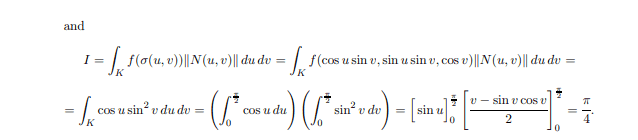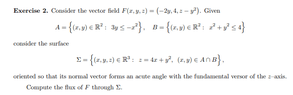SUMMARY
The discussion centers on the application of the Jacobian in spherical coordinates, specifically addressing the surface element in the context of parametrization. The surface area element is derived from the cross product of the partial derivatives of the parametrization function, denoted as ##\boldsymbol{\sigma}##. The Jacobian factor of ##r^2 \sin v## is inherently included in the calculation of the area element, which is expressed as ##dS = |d\boldsymbol{l}_u \times d\boldsymbol{l}_v|##. This confirms that the Jacobian is effectively accounted for in the surface area computation.
PREREQUISITES
- Understanding of spherical coordinates and their parametrization
- Knowledge of vector calculus, particularly cross products
- Familiarity with surface integrals and area elements
- Basic proficiency in mathematical notation and symbols used in calculus
NEXT STEPS
- Study the derivation of the Jacobian in spherical coordinates
- Learn about parametrization techniques in multivariable calculus
- Explore vector calculus applications in surface integrals
- Investigate the role of the cross product in determining area elements
USEFUL FOR
Students and professionals in mathematics, particularly those focusing on multivariable calculus, vector calculus, and geometric applications in physics or engineering.