Which virtual cells look the same as the basic cell?

Click For Summary

Homework Help Overview

The discussion revolves around the concept of virtual cells in the context of mirror reflections, specifically examining how these virtual cells relate to a basic cell defined by real mirrors. The original poster presents a scenario involving a basic cell with a physical object and queries about the appearance and regularity of virtual cells formed by reflections.

Discussion Character

  • Exploratory, Assumption checking

Approaches and Questions Raised

  • The original poster questions the naming of the patterns formed by reflections and the number of reflections needed to illustrate the concept. Some participants suggest simplifying the problem by considering only one reflection per mirror, while others express uncertainty about visualizing multiple reflections.

Discussion Status

The discussion is ongoing, with participants exploring different interpretations of the problem. Some guidance has been offered regarding the approach to take, particularly in limiting reflections to one per mirror, but there is no explicit consensus on how to proceed with the visual representation of the virtual cells.

Contextual Notes

Participants are navigating assumptions about the number of reflections to consider, with some suggesting that an infinite number may not be necessary for the problem at hand. There is also a note that multiple reflections may exist outside the defined virtual cells.

PintoCorreia
Messages
19
Reaction score
0

Homework Statement



fJD1nAu.png


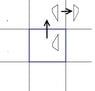
Above is the basic cell drawn with an object inside of it. You look in top view of the basic cell and the space around it filled with virtual cells.


You can see the top view of a basic cell (the square [that is marked blue] formed by the four real mirrors with a height of 10 cm, with the original physical object with a height of 5 cm inside ) and all the copies (mirror images and mirror images of mirror images) around it, which fill a plane.
Question 1: Which virtual cells look the same as the basic cell? Do You see a regularity/pattern?
Explain this mathematically.



Homework Equations


mirror reflections


The Attempt at a Solution


1. I don't understand that whether there is a name for those kind of patterns or not. And How many reflections I should draw. I guess it could be an infinite amount... So anyone a clue?
 
Physics news on Phys.org
Pretend each mirror in turn is the only mirror that exists. eg Just draw one reflection in each cell and see what you get.
 
well, how to image that it gets reflected like 4,5,6 times?
 
I don't think the problem expects you to consider an infinite number of reflections. Just one in each mirror.

This is what I would expect. I've only shown two virtual cells...
 

Attachments

  • Mirrors.jpg
    Mirrors.jpg
    4.5 KB · Views: 452
PS: The multiple reflections (4,5,6 etc) would be located outside the virtual cells.
 

Similar threads

Virtual cells of mirror reflections
  • · Replies 4 ·
Replies
4
Views
2K
Could the Image from the First Mirror Be Real for the Second Mirror?
  • · Replies 7 ·
Replies
7
Views
2K
Is the Solution for Rotation of Spherical Mirrors Incorrect?
  • · Replies 16 ·
Replies
16
Views
2K
Understanding the Math Behind A: Minimum Length of Plane Mirror
  • · Replies 14 ·
Replies
14
Views
4K
Virtual image on the perpendicular
  • · Replies 2 ·
Replies
2
Views
2K
How Does a Combined Lens and Mirror System Create Images?
  • · Replies 1 ·
Replies
1
Views
5K
Virtual boxes mirror reflection
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Virtual and real image with concave mirror at 45 degrees
  • · Replies 4 ·
Replies
4
Views
3K
Engineering Why is my output current so low in this Transconductance Amplifier cell?
  • · Replies 13 ·
Replies
13
Views
3K
Real and virtual images from mirrors
  • · Replies 5 ·
Replies
5
Views
2K