xtimmyx
- 5
- 0
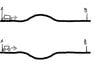
Lets say two wagons is approaching a hill/slope which ends up at the exact same height as before the slope/hill. The wagons are identical and are traveling at the same velocity at point A (approaching the hill/slope). And the hill's/slope's shape is exactly the same but inverted.
Which if any, of the wagons reaches point B first, and which has the highest velocity at that point.
To me it seams logical that its the same for both wagons but as I remember it from a physics assignment in school a couple of years ago that isn't the case and the wagons time/velocity are different at point B.
If so, why?
Which if any, of the wagons reaches point B first, and which has the highest velocity at that point.
To me it seams logical that its the same for both wagons but as I remember it from a physics assignment in school a couple of years ago that isn't the case and the wagons time/velocity are different at point B.
If so, why?