powermind said:
1- The frame O’ moves forward with velocity (v = 0.5c m/s^2) along x-axis with respect to the fixed reference frame O which is a stationary.
2- When two frames O and O’ are coincide, t and t’ are set to 0.
3- A light is located in the frame O’ at x’ = -10m, y’ = 0 and z’ = 0;
4- The light is switched on at 10s according to the frame O’.
I hope it is very clear now and nothing is missing.
It's clear enough that I think I can figure out what you want but first let me point out some problems.
1) You should not specify motion to the frame in which you are specifying your scenario. Since you defined the coordinates of the light in frame O', you should make that your single frame.
2) When you specify a speed as you did under your first bullet, it is sufficient to say v=0.5c. The units of m/s^2 has a couple problems. First, you have seconds squared which isn't appropriate for speed (that's what we need for acceleration). Second, since you're using units of seconds, you probably want to use units for distance of light-seconds. This is also the case for your third bullet.
3) You should say that observer O' is stationary in the frame and observer O is traveling at -0.5c and that they both passed through the origin.
powermind said:
So, λ = 1.154700538, v = 0.5c m/s, x’ of the light = -10m and (t’ = 10s when the light is switched on).
More problems here. You are using the wrong symbol for gamma. You are using Lambda. The symbol you want is γ.
Instead of x' = -10m you should use units of light-seconds and it's obvious that's what you were really doing.
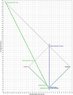
Here's a spacetime diagram depicting everything as I think you want it:
Observer O' is shown in blue and observer O in green. The light is shown in red. Note that O sees the light before O' sees it. Note the times according to their own clocks (the dots represent 1-second intervals of time). O sees it at his own time of about 11.6 seconds and O' sees it at his own time of 20 seconds.
powermind said:
If the time takes 10s according to the frame O’ after the coincidence, the time according to the frame O will take λt' = 11.54700538s.
This isn't correct. You neglected to use the x' value of -10 light-seconds in your calculation. Here is the original spacetime diagram transformed to a speed of -0.5c, making it the rest frame of observer O:
As you can see the time the light turns on in the O frame is around 5.8 seconds and no where near 11 seconds.
powermind said:
Now, when is the light switched on according to the frame O?
The answer is: t = λ(t' + \frac{vx'}{c^2}) = 11.54700536s < 11.54700538s which means that the event occurs first in the frame O then it will occur in the frame O'.
Again, it appears that you used a value of x'=0 in your calculation so it is wrong.
powermind said:
Per the equation t = λt' + λ\frac{vx'}{c^2}, when x’ < 0, t’ >= 0, t is the time of event and λt' is the actual time or current time according to the frame O, then t < λt'. No need to think too much to explore that!
Let us agree to continue …
Let us wait until you get everything right.
But, in the mean time, you should notice that the answer to your question of which observer will see the light first is the same in all frames. In both of the above frames, Observer O' sees the light at his time of 20 seconds and observer O sees it at his time of about 11.6 seconds.
Here is another frame where both observers are traveling at the same speed in opposite directions:
And another frame moving at -0.3c with respect to the original frame:
Note that each observer sees the light according to his own clock the same in all frames. Note that the light propagates at c in all frames. Note that the Coordinate Times and Distances are different in each frame.