Why am I getting the wrong conclusion from my spacetime diagram?

[student34]

On my diagram, a person is traveling in a spaceship to the right in red, which is displayed as a Minkowski diagram . At the origin (0,0) the person traveling travels by a stationary person. And the 2 blue lines are the worldlines of two blue stationary rocks.

But when I try to figure out what the distance is between the rocks from the frame of reference of the spaceship at (0,0), I get a distance wider than the proper length. What am I doing wrong?

 

[PeterDonis]

On my diagram, a person is traveling in a spaceship to the right in red, which is displayed as a Minkowski diagram . At the origin (0,0) the person traveling travels by a stationary person. And the 2 blue lines are the worldlines of two blue stationary rocks.

All of this looks fine.

But when I try to figure out what the distance is between the rocks from the frame of reference of the spaceship at (0,0), I get a distance wider than the proper length. What am I doing wrong?

We can't possibly tell unless you show us your actual calculations.

 

[student34]

All of this looks fine.We can't possibly tell unless you show us your actual calculations.

Without any calculations, it seems that at time = 0 the two blue world lines are actually wider apart for the moving observer than a measurement of them in the rest frame. Aren't they suppose to be closer together because of length contraction?

 

[Ibix]

What am I doing wrong?

At a guess, you calculated $x'$ for each rock at the same $t$ and took the difference, which is larger than the rest spacing by a factor of $\gamma$. But two events with the same $t$ do not have the same $t'$. The rocks are moving in the primed frame, and if you compare the position of one at one time to the position of the other at another time you do not get the separation. If you want their separation as measured in the primed frame you need to measure their positions in that frame at the same time in that frame. That is, you want the difference in $x'$ at the same $t'$, not the same $t$. That separation is smaller by a factor of $\gamma$.

 

[Ibix]

Without any calculations, it seems that at time = 0 the two blue world lines are actually wider apart for the moving observer than a measurement of them in the rest frame. Aren't they suppose to be closer together because of length contraction?

Ok, I was wrong. You just measured the length of red $x'$ axis between the blue lines, which gets you $\sqrt{\Delta x^2+c^2\Delta t^2}$. That is not the length of the line in reality - it's only the length of the line on the diagram. As you may recall from your last very lengthy thread, the Minkowski diagram is a distorted representation of the non-Euclidean Minkowski plane. That means you can't just measure lengths on the diagram and hope. You need to calculate.

Remember that the length of a spacelike line is $\sqrt{\Delta x^2-c^2\Delta t^2}$, not $\sqrt{\Delta x^2+c^2\Delta t^2}$.

 

[PeterDonis]

Without any calculations, it seems

You can't just look at spacetime diagrams and judge by what "seems" to be the case. The geometry of Minkowski spacetime is not the same as the geometry of a Euclidean space, which is what your "seems" intuition is used to. You need to actually do the math.

 

[Sagittarius A-Star]

But when I try to figure out what the distance is between the rocks from the frame of reference of the spaceship at (0,0), I get a distance wider than the proper length. What am I doing wrong?View attachment 302707

The x-axis and the x'-axis have different scales.

As illustrated in Fig 2-3, the boosted and unboosted spacetime axes will in general have unequal unit lengths. If U is the unit length on the axes of ct and x respectively, the unit length on the axes of ct′ and x′ is:[6]
$U'=U{\sqrt {\frac {1+\beta ^{2}}{1-\beta ^{2}}}}$

Source:
https://en.wikipedia.org/wiki/Spacetime_diagram#Mathematical_detailsYou can see length contraction in a Minkowski diagram in both directions in Fig. 7.10 on page 56 of the book "Freund, Jürgen (2008). Special Relativity for Beginners".

Google books preview using Chrome:
https://books.google.de/books?id=-Mw7DQAAQBAJ&lpg=PA52&hl=de&pg=PA56#v=onepage&q&f=false

 

[Orodruin]

As others have already said, you are likely ignoring the fact that Minkowski spacetime has a different geometry than Euclidean space. Instead of the Pythagorean theorem $l^2 = x^2 + y^2$ you have $l^2 = x^2 - c^2 t^2$. In Euclidean space you can find the normalization of the axes by drawing a circle of radius one. Checking where the circle crosses an axis will give you the ”1” tick on the axis because of the Pythagorean theorem.

In Minkowski space you instead need to draw the hyperbola corresponding to $1= x^2-c^2t^2$. Where this hyperbola intersects the $x’$ axis will correspond to $x’=1$. Because of how a hyperbola works, this will occur at $x>1$.

 

[Sagittarius A-Star]

Minkowski With One Pt and Hyperbolic Arc

Source:
https://www.geogebra.org/m/NnrRvA46

 

[vanhees71]

On my diagram, a person is traveling in a spaceship to the right in red, which is displayed as a Minkowski diagram . At the origin (0,0) the person traveling travels by a stationary person. And the 2 blue lines are the worldlines of two blue stationary rocks.

But when I try to figure out what the distance is between the rocks from the frame of reference of the spaceship at (0,0), I get a distance wider than the proper length. What am I doing wrong?View attachment 302707

That's the problem with Minkowski diagrams. You must forget about reading them as if they were in a Euclidean plane. They are instead in a "Minkowskian plane". You have to construct the unit distances for your axes using the correponding time-like and space-like hyperbolae. Then you'll see that the distance measured in the primed system is indeed smaller by an inverse Lorentz factor than the distance measured in the unprimed frame, were the two rockets are both at rest.

See Fig. 2 (right panel) for the Minkowski diagram to illustrate length contraction in

https://itp.uni-frankfurt.de/~hees/pf-faq/srt.pdf

 

[Sagittarius A-Star]

But when I try to figure out what the distance is between the rocks from the frame of reference of the spaceship at (0,0), I get a distance wider than the proper length. What am I doing wrong?View attachment 302707

In the following overlay of GeoGebra and your diagram, you can see scales at the axes.

$\beta \approx \tan (25.5) \approx 0.477$
$1/\gamma \ \approx 0.88$
$L = 3, \ \ \ L' = 2.64$ (measured at events A and B).

Now consider a rod between events A and B, that is at rest in the spaceship and has the length M' = L'. Length contraction of the rod in the stationary frame:
$M' = 2.64, \ \ \ M = 2.32$.

 

[student34]

The x-axis and the x'-axis have different scales.Source:
https://en.wikipedia.org/wiki/Spacetime_diagram#Mathematical_detailsYou can see length contraction in a Minkowski diagram in both directions in Fig. 7.10 on page 56 of the book "Freund, Jürgen (2008). Special Relativity for Beginners".

Google books preview using Chrome:
https://books.google.de/books?id=-Mw7DQAAQBAJ&lpg=PA52&hl=de&pg=PA56#v=onepage&q&f=false

Thanks, I did not know that they were different scales. It makes sense now.

 

[student34]

Ok, I was wrong. You just measured the length of red $x'$ axis between the blue lines, which gets you $\sqrt{\Delta x^2+c^2\Delta t^2}$. That is not the length of the line in reality - it's only the length of the line on the diagram. As you may recall from your last very lengthy thread, the Minkowski diagram is a distorted representation of the non-Euclidean Minkowski plane. That means you can't just measure lengths on the diagram and hope. You need to calculate.

Remember that the length of a spacelike line is $\sqrt{\Delta x^2-c^2\Delta t^2}$, not $\sqrt{\Delta x^2+c^2\Delta t^2}$.

I think this is wrong because on the x' axis $\sqrt{\Delta x^2-c^2\Delta t^2}$ should be $\sqrt{\Delta x^2-0}$

 

[PeroK]

I think this is wrong because on the x' axis $\sqrt{\Delta x^2-c^2\Delta t^2}$ should be $\sqrt{\Delta x^2-0}$

On the $x$ axis we have $\Delta t = 0$ (by definition), so the spacetime length reduces to the proper length $|\Delta x|$.

On the $x'$ axis we have $\Delta t' = 0$ (by definition) but never $\Delta t = 0$.

 

[Sagittarius A-Star]

I think this is wrong because on the x' axis $\sqrt{\Delta x^2-c^2\Delta t^2}$ should be $\sqrt{\Delta x^2-0}$

On the x'-axis length is $\sqrt{\Delta {x'}^2-0} = \sqrt{\Delta x^2-c^2\Delta t^2}$. Reason is that the squared spacetime-interval is invariant:
$$\Delta {x'}^2-c^2\Delta {t'}^2 = \Delta x^2-c^2\Delta t^2$$

 

[student34]

On the $x$ axis we have $\Delta t = 0$ (by definition), so the spacetime length reduces to the proper length $|\Delta x|$.

On the $x'$ axis we have $\Delta t' = 0$ (by definition) but never $\Delta t = 0$.

I don't understand what you are saying here. Why can't $\Delta t = 0$ ?

 

[Sagittarius A-Star]

Why can't $\Delta t = 0$ ?

In the diagram of posting #11 you can see, that events A and B are simultaneously in the spaceship's frame, but not simultaneously in the "stationary" frame.

 

[PeroK]

I don't understand what you are saying here. Why can't $\Delta t = 0$ ?

Because you are on the $x'$ axis. No two points on the $x'$ axis have the same $t$ coordinate.

 

[student34]

That's the problem with Minkowski diagrams. You must forget about reading them as if they were in a Euclidean plane. They are instead in a "Minkowskian plane". You have to construct the unit distances for your axes using the correponding time-like and space-like hyperbolae. Then you'll see that the distance measured in the primed system is indeed smaller by an inverse Lorentz factor than the distance measured in the unprimed frame, were the two rockets are both at rest.

See Fig. 2 (right panel) for the Minkowski diagram to illustrate length contraction in

https://itp.uni-frankfurt.de/~hees/pf-faq/srt.pdf

Thanks, the diagram is very helpful to visualize why the units are bigger on the x' axis. This is all starting to make sense now.

 

[student34]

Because you are on the $x'$ axis. No two points on the $x'$ axis have the same $t$ coordinate.

Oh yes, I thought you meant in general.

 

[robphy]

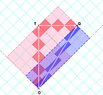
Here's another spacetime diagram that might help.

By using "rotated graph paper",
many calculations can be done by counting and doing very simple arithmetic.
The boxes in the grid ("light-clock diamonds") are based on the light-clock of the observer at rest who draws this diagram.

By forming the "causal diamond" where your events are opposite corners
and the diamond-edges are along the lightcone, the area of the diamond (in units of the light-clock diamond) gives the square-interval between those events. The square-root of the magnitude gives the "length" along the diagonal of the diamond.

I tried to reconstruct the situation you have drawn.
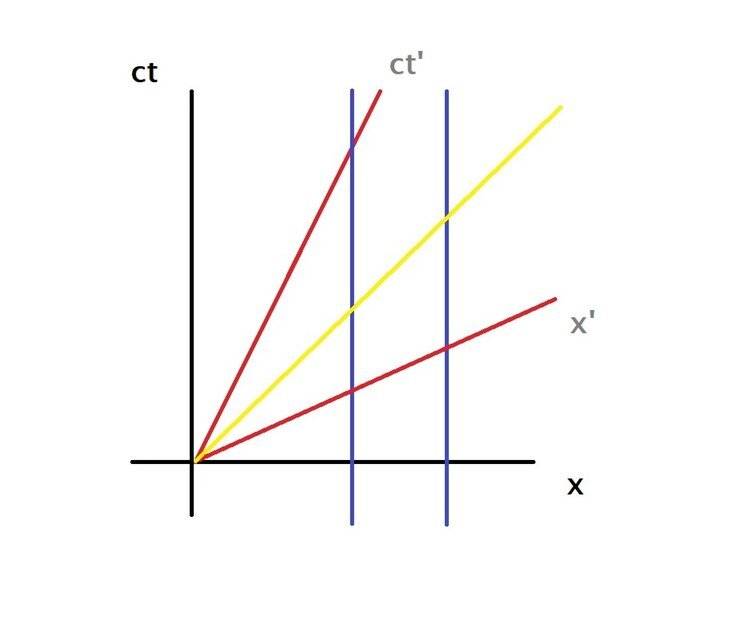
It seems that your moving frame moves at $v=(0.5)c$, and your rocks are at $x=5$ and $x=8$.
By computing the areas, you can see that the moving frame measures a shorter distance between the parallel worldlines.

(t,x) coordinates: P1=(2.5, 5) and P2=(4,8)
The square-interval (using the $(+,-,-,-)$-convention ) is $(4-2.5)^2-(8-5)^2= -6.75$

Note: for $v=(1/2)c$, we have $\gamma=\frac{1}{\sqrt{1-v^2}}=\sqrt{4/3}$. Furthermore,
$$(\ell')^2=\frac{\ell^2}{\gamma^2}=\frac{9}{4/3}=(27/4)=6.75$$

If you choose nice numbers (like $v=(3/5)c$, which have rational Doppler factors, here $k=2$
(whereas $v=(1/2)c$ has $k=\sqrt{3}$)), the arithmetic is easier (especially when used with nicer intervals, like 5 (rather than 3) for $v=(3/5)c$) and the visualization of the ticks along the segments is easier... assuming the primary goal is to first have an understanding of what is going on... before moving on to solving more general problems.

With $v=(3/5)c$ (so, $k=\sqrt{\frac{1+v}{1-v}}$ and $\gamma=\frac{1}{\sqrt{1-v^2}}=5/4$)
and $\ell=5$ (between $x=5$ and $x=10$).

For more on this approach, consult my Insights (first link in my signature below).

 

[Sagittarius A-Star]

By forming the "causal diamond" where your events are opposite corners
and the diamond-edges are along the lightcone, the area of the diamond (in units of the light-clock diamond) gives the square-interval between those events. The square-root of the magnitude gives the "length" along the diagonal of the diamond.

In the Minkowski diagram you can also construct an area (based on a non-rotated graph paper), which is the squared interval between those events. It is the area of the rhombus (symmetrical with regards to the light world lines), with the events at neighboring points, in the following link events C and B:
https://www.geogebra.org/m/dYyg5ZB8#material/ewe6t2BU

Proof:
https://www.geogebra.org/m/HCBWqpjY

See also:
http://www.dierck-e-liebscher.de/images/geometrie/minkowski-pythagoras.html

 

[robphy]

In the Minkowski diagram you can also construct an area (based on a non-rotated graph paper), which is the squared interval between those events. It is the area of the rhombus (symmetrical with regards to the light world lines), with the events at neighboring points, in the following link events C and B:
https://www.geogebra.org/m/dYyg5ZB8#material/ewe6t2BU

Yes!
In fact, any area in the diagram is preserved by a boost (since the determinant of the boost equals 1).

One advantage of the "causal diamond" is that the events themselves (not just the size of the area) in the diamond have an invariant definition...

• Along the timelike diagonal, the diamond is formed as
  the intersection
  of the future (light cone and interior) of the past vertex
  and the past of the future vertex.
  Physically, the events in that diamond can be influenced by the past vertex and can also influence the future vertex.
  When the diamond of CB is constructed in all spacetime diagrams,
  those set of events are the same, along with the size of the area,
  although the "shape" of the diamond will differ.
  (The shape is determined by the relative Doppler factors... as shown below.)

For the "coordinate rhombi" (my term) with edges along the coordinate tickmarks,
those rhombi make reference to the tickmarks of that observer.
The events along a rhombus edge are the same coordinate value for that observer (but not for other observers in general).
Of course, the two grids are compatible and can be obtained
by slicing them up into triangles are rearranging.

I think a key difference is that, once understood, the construction of the diamonds
and subsequent calculations based on counting diamonds are easier.
For example, one never has to explicitly calculate $\gamma$.

---

For comparison with the diagram from your first link,

• 

• here's my version of the Pythagorean theorem.
  
  
  $(area CT)^2-(area TB)^2=(area CB)^2=25-9=16$.

I think the area of the causal diamond of CB is clearly gotten
by easily counting the 16 diamonds in the rotated grid.

In fact, using only the diamonds in the causal diamond of CB,
observe the following.

• With the red clock diamonds, diamond CB has u=8 and v=2,
  with aspect ratio $u/v=8/2=k^2$ so $k=2$.
  Since $k=\sqrt{\frac{1+v}{1-v}}$, then $v=\frac{k^2-1}{k^2+1}=3/5$
  (in agreement with what is determined by $TB/CT$).
  Since the area is $uv=(8)(2)$, the square interval is 16
  (in agreement with what is determined by $(CT)^2-(TB)^2=\left(\frac{u+v}{2}\right)^2-\left(\frac{u-v}{2}\right)^2=5^2-3^2$).
• With the blue clock diamonds, diamond CB has u=4 and v=4,
  with aspect ratio $u/v=4/4=k^2$ so $k=1$.
  Since $k=\sqrt{\frac{1+v}{1-v}}$, then $v=\frac{k^2-1}{k^2+1}=0$,
  which means that CB is at rest with respect to
  the observer along the timelike diagonal of the blue diamonds.
  Since the area is $uv=(4)(4)$, the square interval is 16
  (in agreement with what is determined by $\left(\frac{u+v}{2}\right)^2-\left(\frac{u-v}{2}\right)^2=4^2-0^2$)).

The blue clock diamond obtained by stretching the red diamond by a factor of k=2 in the forward direction and shrinking by that factor (so the area is unchanged) is a Lorentz boost in the eigenbasis… in light-cone coordinates.

---

For a more detailed example of a diagram and calculation using the diamonds
look at page 9 of my slides (from an old talk) describing an elastic collision
https://www.aapt.org/docdirectory/m...aper-CalculatingWithCausalDiamonds.pdf#page=9
On one diagram, it features 4 reference frames (the lab frame, the two frames for the initial particles, and one frame for one of the final particles)... the 5th frame is not yet determined until the problem is solved
...by counting diamonds,

 

[robphy]

See also:
http://www.dierck-e-liebscher.de/images/geometrie/minkowski-pythagoras.html

Liebscher has a very nice book.

The Geometry of Time by Dierck-Ekkehard Liebscher

(Although the one Amazon review didn't like it,
I think it has many geometrical insights that are not found anywhere else.
As it says in the inside flap, " its aim is to show the connection with synthetic geometry".
If the reader is not interested in that aspect, then this work would not be appreciated by that reader.)

(In the book, the link to Reference 7 is outdated.)

 

[vanhees71]

It's of course clear that the usual Minkowski diagram and the "rotated graph paper" are finally equivalent. It's just using different coordinates for the Minkowksi plane: In the case of the Minkowski diagram one uses pseudo-Cartesian (Lorentzian) coordinates in the "rotated graph paper" the underlying coordinates behind this formulation of SR (Bondi calculus) are light-cone coordinates.

That areas occur is natural in hyperbolic geometry. It's because in the parametrization of the unit hyperbola $(\cosh \eta,\sinh \eta)$, $\eta$ is an area, and that's why the inverse functions of the hyperbolic functions are called area functions (arsinh, arcosh, artanh).