- #1
- 2,168
- 193
I am trying to understand the basic conceptual ideas about the space-time diagrams. In spacetime diagrams we have events which are labeled as points on the diagram.
Let us call we have an event on point ##A(0,0)##and another event on ##B(4,0)## measured by an inertial frame ##S##. This inertial frame sees another inertial frame ##S'## which moves with a speed of ##V = 0.6c## in the ##+x## direction. Let us draw this.
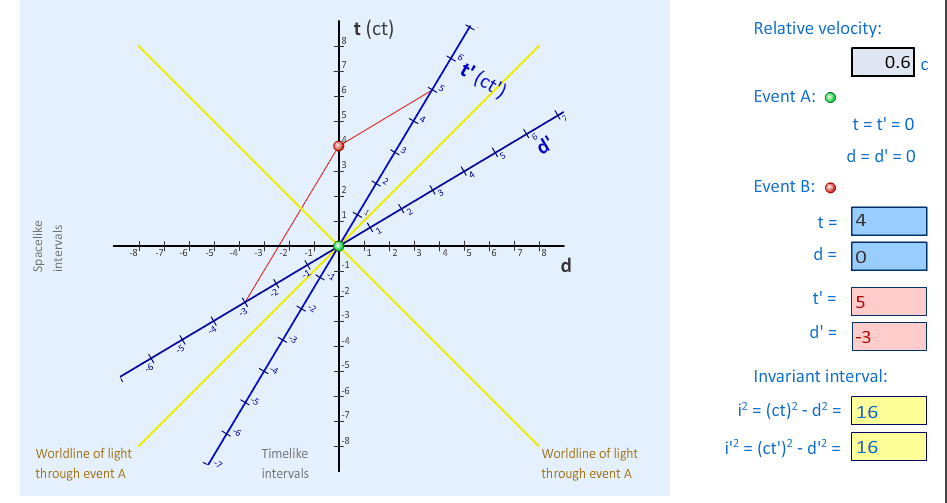
I learned that in the SR diagram if there are two timelike geodesics the longest length belongs to the one which is the straigthest. So If ##S## is at rest, the proper time of the ##S'## must be shorter. But in this picture its higher. How is it possible ?
How are we labeling these events or what they are measuring ? I am so confused that I cannot even explain what I am really confused about. I know lorentz transformations but I am more confused about who measures which quantity, how is it labeled in the spacetime diagram. Since we are drawing the graph that shows that ##S## is at rest, is that mean all the measurements done by ##S##? If so what does it mean ##t'=5## ? Does it says ##S'## measures its proper time as ##5## or does it says ##S## measures ##S'## proper time as ##5##.
So ##S## measures an event at ##B(4,0)##he calculates the proper time between events, ##A##and ##B##,
$$\tau(A,B) = \int_A^B \sqrt{-g(d\vec{x}, \vec{x})} = \int_A^B\sqrt{dt - V^2dt^2} = (t_B - t_A)\sqrt{1-V^2} = 4 $$
Now ##S## wants to calculate the proper time of the ##S'##. What is the proper time equation that we can write for this case and why ?
Let us call we have an event on point ##A(0,0)##and another event on ##B(4,0)## measured by an inertial frame ##S##. This inertial frame sees another inertial frame ##S'## which moves with a speed of ##V = 0.6c## in the ##+x## direction. Let us draw this.
I learned that in the SR diagram if there are two timelike geodesics the longest length belongs to the one which is the straigthest. So If ##S## is at rest, the proper time of the ##S'## must be shorter. But in this picture its higher. How is it possible ?
How are we labeling these events or what they are measuring ? I am so confused that I cannot even explain what I am really confused about. I know lorentz transformations but I am more confused about who measures which quantity, how is it labeled in the spacetime diagram. Since we are drawing the graph that shows that ##S## is at rest, is that mean all the measurements done by ##S##? If so what does it mean ##t'=5## ? Does it says ##S'## measures its proper time as ##5## or does it says ##S## measures ##S'## proper time as ##5##.
So ##S## measures an event at ##B(4,0)##he calculates the proper time between events, ##A##and ##B##,
$$\tau(A,B) = \int_A^B \sqrt{-g(d\vec{x}, \vec{x})} = \int_A^B\sqrt{dt - V^2dt^2} = (t_B - t_A)\sqrt{1-V^2} = 4 $$
Now ##S## wants to calculate the proper time of the ##S'##. What is the proper time equation that we can write for this case and why ?