Why Are My Coupled Oscillator Eigenvalues Incorrect?

[Redwaves]

Homework Statement

What are the eigenvalue and eigenvectors
$m_a = m_b = m_c$

Relevant Equations

$\frac{d^2x_a}{dt^2} + \frac{2kx_a}{m} - \frac{kx_b}{m}$

$\frac{d^2x_b}{dt^2} + \frac{3kx_b}{m} - \frac{kx_a}{m} - 2\frac{kx_c}{m}$

$\frac{d^2x_c}{dt^2} + \frac{2kx_c}{m} - \frac{2kx_b}{m}$

Hi,
I have to find the eigenvalues and eigenvectors for a system of 3 masses and 4 springs. At the end I don't get the right eigenvalues, but honestly I don't know why. Everything seems fine for me. I spent the day to look where is my error, but I really don't know.

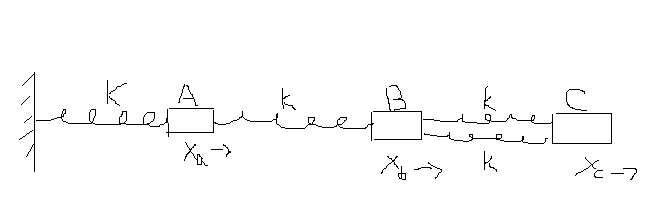
$m_a = m_b = m_c$

I got these motion equations

$\frac{d^2x_a}{dt^2} + \frac{2kx_a}{m} - \frac{kx_b}{m} = 0$

$\frac{d^2x_b}{dt^2} + \frac{3kx_b}{m} - \frac{kx_a}{m} - 2\frac{kx_c}{m} = 0$

$\frac{d^2x_c}{dt^2} + \frac{2kx_c}{m} - \frac{2kx_b}{m} = 0$

Then, after plugging the solution $x(t) = X_{ni} cos(\omega_n + \alpha_n)$

I get this matrix

$\begin{pmatrix} -\omega_n^2 +\frac{2k}{m} & -\frac{k}{m} & 0\\ - \frac{k}{m} & -\omega_n^2 +\frac{3k}{m} & -\frac{2k}{m} \\ 0 & -\frac{2k}{m} &-\omega_n^2 +\frac{2k}{m} \end{pmatrix}$

Next, I have to find that $det(A)$ = 0
$(-\omega_n^2 + \frac{2k}{m})[(-\omega_n^2 + \frac{3k}{m})^2 -(\frac{2k}{m})^2 - (\frac{k}{m})^2 ] = 0$

thus,
I have $\omega_1^2 = \frac{2k}{m}, \omega_2^2 = -\frac{k}{m}(-3 -\sqrt{5}), \omega_3^2 = -\frac{k}{m}(-3 +\sqrt{5})$

However the correct eigenvalues are
I have $\omega_1^2 = \frac{2k}{m}, \omega_2^2 = \frac{5-\sqrt{21}}{2}\frac{k}{m}, \omega_3^2 = \frac{5+\sqrt{21}}{2}\frac{k}{m}$

 

[haruspex]

I don't see how you got that polynomial from expanding the determinant. In particular, how do you get a term
$(-\omega_n^2 + \frac{3k}{m})^2$
?
I get the book answer, except I get 24s instead of 21s.

 

[kuruman]

I don't see how you got that polynomial from expanding the determinant. In particular, how do you get a term
$(-\omega_n^2 + \frac{3k}{m})^2$
?
I get the book answer, except I get 24s instead of 21s.

I agree that the $(-\omega_n^2 + \frac{3k}{m})^2$ term does not belong. However, the determinant I got gives the book's eigenvalues.

 

[Redwaves]

I agree that the $(-\omega_n^2 + \frac{3k}{m})^2$ term does not belong. However, the determinant I got gives the book's eigenvalues.

My bad after checking for 100 times I see my error. I replaced $(-\omega_n^2 + \frac{3k}{m})^2$ with $(-\omega_n^2 + \frac{2k}{m})^2$
I'm so frustrated I spent all day just for that.
Thanks guys

 

[kuruman]

My bad after checking for 100 times I see my error. I replaced $(-\omega_n^2 + \frac{3k}{m})^2$ with $(-\omega_n^2 + \frac{2k}{m})^2$
I'm so frustrated I spent all day just for that.
Thanks guys

I don't see how one gets $(-\omega_n^2 + \frac{2k}{m})^2$ out of this.

When I am faced with the eigenvalues of a matrix larger than 2×2, I try to find common factors in the characteristic equation before multiplying out any terms in parentheses. In this case, expanding the determinant along the top row gives $$\left(\frac{2 k}{m}-\omega_n^2 \right)\left[\left(\frac{3 k}{m}-\omega_n^2 \right)-\frac{4 k^2}{m^2}\right] +\frac{k}{m} \left[-\frac{k}{m}\left(\frac{2k}{m}-\omega_n^2\right)\right]=0.$$There is an obvious common factor $\left(\frac{2 k}{m}-\omega_n^2 \right)$ which provides the first eigenvalue $\omega_1^2=2k/m$. To find the other two eigenvalues, we assert that $\omega_n^2\neq2k/m$ and divide the equation by the common factor to get $$\left(\frac{3 k}{m}-\omega_n^2 \right)-\frac{5 k^2}{m^2} =0.$$Solving the quadratic is trivial.

 

[Redwaves]

I don't see how one gets $(-\omega_n^2 + \frac{2k}{m})^2$ out of this.

When I am faced with the eigenvalues of a matrix larger than 2×2, I try to find common factors in the characteristic equation before multiplying out any terms in parentheses. In this case, expanding the determinant along the top row gives $$\left(\frac{2 k}{m}-\omega_n^2 \right)\left[\left(\frac{3 k}{m}-\omega_n^2 \right)-\frac{4 k^2}{m^2}\right] +\frac{k}{m} \left[-\frac{k}{m}\left(\frac{2k}{m}-\omega_n^2\right)\right]=0.$$There is an obvious common factor $\left(\frac{2 k}{m}-\omega_n^2 \right)$ which provides the first eigenvalue $\omega_1^2=2k/m$. To find the other two eigenvalues, we assert that $\omega_n^2\neq2k/m$ and divide the equation by the common factor to get $$\left(\frac{3 k}{m}-\omega_n^2 \right)-\frac{5 k^2}{m^2} =0.$$Solving the quadratic is trivial.

I meant, in the matrix at position 2ij, I replaced 2k/m with 3k/m in the determinant formula.

 

[kuruman]

That will do it. Thanks for the clarification.