Why are my integrals giving different results for the same function?

[MartinV05]

I've been solving this exercise and I came to a point when one function can get two different integrals:

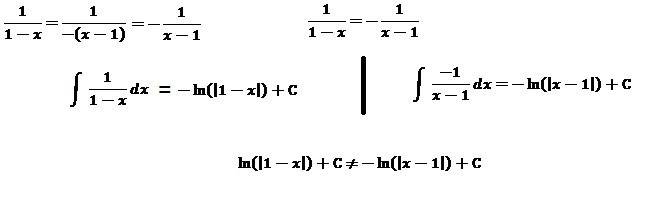
Am I doing something wrong? Because both functions are the same, and the integrals (indefinite) are really different. This is a huge problem, because this is almost the final step of an exercise and when I exchange the current variable (x) with the previously defined function for it, the solution is VERY different.
**There should be a "-" in front of the last line of equation in the picture.

 

[HallsofIvy]

No, the two integrals are NOT "really different"- they are identical. |x- 1|= |1- x| so, of course, -ln(|x-1|)+ C= -ln(|1- x|)+ C.

 

[Redbelly98]

Since you are taking the absolute value, |1-x| and |x-1| are the same.

 

[MartinV05]

In the final expression a "-" appears, but I don't see how we can just make it go away (turn positive) when we are working with variables. The variable can be +-∞.

 

[Redbelly98]

The final expressions both have a "-". There is no need to make it go away.