synkk
- 216
- 0
For part b:
Could anyone why it is + or - 3? I really don't understand why there would be two solutions as det|P| as it would just be the absolute value of P, meaning just +ve?
It's "±" because your equation has the absolute value of the determinant of p .synkk said: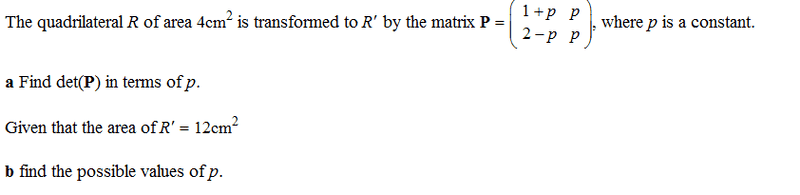
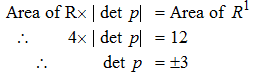
For part b:
Could anyone why it is + or - 3? I really don't understand why there would be two solutions as det|P| as it would just be the absolute value of P, meaning just +ve?
You seem to be confusing P (the matrix) and p (a number). Uppercase and lowercase are significant here, and you seem to be ignoring the difference.synkk said: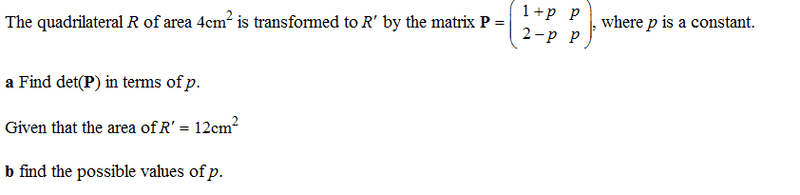
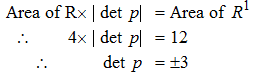
For part b:
Could anyone why it is + or - 3? I really don't understand why there would be two solutions as det|P| as it would just be the absolute value of P, meaning just +ve?
SammyS said:It's "±" because your equation has the absolute value of the determinant of p .
Mark44 said:You seem to be confusing P (the matrix) and p (a number). Uppercase and lowercase are significant here, and you seem to be ignoring the difference.
The notation |P| doesn't mean "absolute value" of P; it is the determinant of P, also written as det(P).
What you show as |det p| makes no sense, because you're not taking the deteriminant of the number p - you want the determinant of the matrix P.
OK, then that's an error in the book. Apparently the author got confused between P and p.synkk said:What is shown in the OP is what the book has shown, not me.
synkk said:Thanks for your input so far.
SammyS said:It's "±" because your equation has the absolute value of the determinant of p .
synkk said:Why?
SammyS said:The solution to
4|x|=12
is
x = ±3 .
Do you agree?
synkk said:No I've never learned this before, could you explain it please?
d2j2003 said:the solution to 4|x|=12 is x=±3 BECAUSE if you plug x back in it works for both 3 and -3 ie. if you only list one of these as a solution then you have not completely solved the equation.
Therefore if you have 4|det P|=12 then |det P| = 3 meaning that det P can be either 3 or -3
make sense?