Why can we ignore certain circuit paths?

[xAly]

Homework Statement

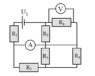
We have to determine the readings on the ammeter and voltmeter (see picture of circuit), given that $\text{R}_1 = 4 \Omega, \text{R}_2 = 10 \Omega, \text{R}_3 = 7 \Omega, \text{R}_4 = 8 \Omega, \text{R}_5 = 6 \Omega, \text{R}_6 = 3 \Omega$

Relevant Equations

$\text{R} = \frac{\text{V}}{\text{I}}$, Resistance in parallel and series.

I get really confused with these types of problems. I don't know how to break down the circuit properly. I tried to go anticlockwise and ignored the ammeter and the voltmeter as circuit components, which gave me R1 and R2 in series while R3 and R5 (in series) are in parallel with R4 and R6 (also in series). This gave me a final equivalent resistance of $\frac{479}{24}$. But after checking my intermediate solution, it seems this approach is wrong. The solution starts with stating that we can ignore the lower half of the circuit and can only consider the resistors R1, R5 and R6 (so the problem becomes a lot easier). However I don't see why this is true and how one would spot this in similar problems.

 

[mfb]

An (ideal) amperemeter is a perfect conductor. You can replace it by a wire in the circuit analysis.

 

[xAly]

An (ideal) amperemeter is a perfect conductor. You can replace it by a wire in the circuit analysis.

I still don't see how I can ignore the lower half of the circuit. Surely the current will still split up at the first junction?

 

[jbriggs444]

I still don't see how I can ignore the lower half of the circuit. Surely the current will still split up at the first junction?

If the ammeter is treated as a perfect conductor then the potential at all three nodes to the left and right of the ammeter must be identical.

If the potential at all three nodes is identical then no current will flow through any resistors in the bottom half of the circuit. A circuit element through which no current flows might as well not be there. Remove it, leaving stub wires and an open circuit in its place. Then remove the stubs.

 

[mfb]

This is the circuit with the amperemeter replaced by a wire and the voltmeter removed:

No current will flow through the lower resistors.

 

[xAly]

This is the circuit with the amperemeter replaced by a wire and the voltmeter removed:

View attachment 247589

No current will flow through the lower resistors.

Sorry, I am still quite not following. How does one justify the fact that there is no current? Jbriggs mentioned the fact that the potential must be the same at all the nodes, but isn't a wire also a perfect conductor and so there wouldn't be a current through the horizontal wire at all?

 

[jbriggs444]

Sorry, I am still quite not following. How does one justify the fact that there is no current? Jbriggs mentioned the fact that the potential must be the same at all the nodes, but isn't a wire also a perfect conductor and so there wouldn't be a current through the horizontal wire at all?

Current flows through wires just fine. If there is any potential difference at all, an infinite current will flow. That is precisely why no potential difference can exist between two points on a wire.

 

[FactChecker]

The ammeter completely short-circuits the lower part. There is no potential difference across the ammeter because enough current flows through the ammeter at zero resistance to equalize the potential. Since there is no potential difference, there will be no (resisted) current flow on the lower path.
Mathematically, the fraction of current through path #1 in two parallel circuits is $\frac {\frac {1}{R_1}}{\frac {1}{R_2} + \frac {1}{R_1}} = \frac {R_2}{R_1+R_2}$

(see Figure 1 of Current Divider)

 

[DaveE]

You can tell that there is no current flow in the lower half because if the voltage difference across a resistor (or a network of resistors) is zero then the current must also be zero. V = I*R. If the current through a resistor is zero, or the voltage across a resistor is zero (they are the same thing), then it doesn't matter what it's value is, so you can substitute whatever you want from 0 to ∞ without changing the solution to the problem. Yes, you are changing the circuit, but you are changing it to a circuit with exactly the same solution as the original one.

 

[sojsail]

I found this to be an interesting discussion. I can not tell if the worry has been eliminated, so I would like to add my way of seeing that.

Current would be flowing down the schematic thru R1. Let the potential of the "horizontal wire" be Vh. What if some current tried to continue going down the drawing toward R2? That is a 10Ω resistor, so that current would be stymied -- unless the potential at the right end of R2 was lower than Vh. That is the only way positive charge has the attraction to the other end of a resistor. Well assume for now that it is lower there and call that Vr2r. Then what? That current would then have to go up R3 and/or R4. But that could only happen if the other end of R3 and R4 were lower than Vr2r. BUT, it is higher than Vr2r, because it is Vh! So that blows this whole "what if" story out of the water.