Why do distant objects appear to move more slowly?

[adjacent]

Homework Statement

This is not really a homework question and I am not sure if this should be in the Maths forum or Physics forum.


See the title.
For example,a plane with the same length and speed is moving at constant speed near and far away from me.
From my experience I know that the far plane will appear to move more slowly.Why?

The Attempt at a Solution

I have seen many people saying that as the distance from the eye increases,the distance the plane have to move across the field of view increases.That's why it is moving slowly.
This does not make much sense to me.
I don't have a proof based understanding of this.

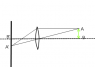
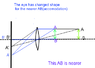
One idea that came to my mind is that as the distance from the eye increases,as the plane goes from a point A to B(Eye is C),the angle ACB is less than the angle ACB it makes when it moves nearer to me.
So as the angle is less, the distance it moves on the image is less.
(I can't explain this so well but I hope you understand what I mean)

My explanation seems too childish.If it's right,can you make it make sense Mathematically?

 

[PhysicoRaj]

My explanation seems too childish.If it's right,can you make it make sense Mathematically?

Your idea already seems mathematical for me. Math doesn't always mean equations and operations. It is also logic. You have used (knowingly or unknowingly) the math that is needed. Still, this could be connected to mathematical equations as S=rΘ.

 

[adjacent]

Still, this could be connected to mathematical equations as S=rΘ.

What is S=rΘ?

 

[PhysicoRaj]

What is S=rΘ

Actually it is the consequence of the definition of the plane angle, how we made it.
Any plane angle, Θ is defined as the ratio of the arc length of a circle which subtends the angle Θ, to the radius of the circle.
If S is the arc length, r the radius then
Θ=S/r
S=rΘ

Note that Θ is in radians.

 

[adjacent]

Actually it is the consequence of the definition of the plane angle, how we made it.
Any plane angle, Θ is defined as the ratio of the arc length of a circle which subtends the angle Θ, to the radius of the circle.
If S is the arc length, r the radius then
Θ=S/r
S=rΘ

Note that Θ is in radians.

But if light is being refracted by the lens,why not use the refraction formula?
$$n_1\sin(i)=n_2\sin(r)$$

What's the use of S=rΘ here?

 

[PhysicoRaj]

But if light is being refracted by the lens,why not use the refraction formula?
$$n_1\sin(i)=n_2\sin(r)$$

What's the use of S=rΘ here?

I'm not sure if I got you right.. by refraction formula, how do you prove that farther objects appear to move slowly?

 

[adjacent]

I'm not sure if I got you right.. by refraction formula, how do you prove that farther objects appear to move slowly?

No.Not the refraction formula,sorry.I'll use a ray diagram.

Then I will do a little trigonometry to prove it.

 

[PhysicoRaj]

So your object moves from A to B while the image moves from A^' to B^' and A^'B^' is smaller than AB hence it appears to move slowly, right?
If you do the trigonometry, you'll end up with something similar to S=rΘ only that the angle Θ will be inside a trig function.

 

[adjacent]

So your object moves from A to B while the image moves from A^' to B^' and A^'B^' is smaller than AB hence it appears to move slowly, right?

No it's not like that.

The AB is closer than AB(Note the colour difference)
So as the plane move from A to B,the image moves from A' to B'.
When the plane move from A to B,the image move from A' to B' and the distance A'B' is greater than A'B'.So the far plane takes a longer time to move across the retina than the near plane.The rest is handled by the brain

 

[PhysicoRaj]

I get it. This is nothing but the use of $S=rθ$ here. If you would look into the derivation for the magnification of a simple microscope (the lens here) you can observe that the angle subtended by the object at the eye, and at the lens is considered. Not getting into details, we can deduce that relation to meet our needs, and it clearly yields $\tan θ = \frac{h}{D}$ where $h$ is equivalent to $S$ and $D$ to $r$. $\tan θ$ can be approximated to $θ$ for small angles. Fetching $θ=\frac{S}{r}$

Since $S$ is constant, $\theta$ is inversely proportional to $r$. Hence as distance, $r$ increases, $\theta$ decreases. It's 'angular velocity' decreases.

 

[adjacent]

Thank you so much
PhysicoRaj.
I think I understand it now