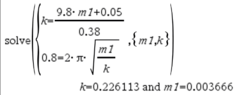Why Do I Get Negative Values Solving the SHM Spring Problem?

[torinketo]

Homework Statement

A block of unknown mass is attached to the end of a vertical spring. When a second 50 g block is suspended, the spring extends by 38 cm. The oscillation period without the second 50 g block is 0.8 s. Find:

(a) the spring constant of the spring (in N/m);
(b) the mass of the first block (in kg).

Relevant Equations

T=2pi*sqrt(m/k)
k=mg/x

m1 = unknown
m2 = 0.05 kg
x = 0.38 m
T = 0.8s

Tried to plug in values into the above equations:

0.8 = 2pi*sqrt(m1+0.05/k)
k = ((m1+0.05)*9.8)/0.38

Got negative values for both k and m which doesn't make sense

 

[haruspex]

0.8 = 2pi*sqrt(m1+0.05/k)

The 0.8 seconds is for m1 by itself.

k = ((m1+0.05)*9.8)/0.38

It's not clear whether the 0.38m is for the masses together or just the 50g mass.

 

[torinketo]

The 0.8 seconds is for m1 by itself.

It's not clear whether the 0.38m is for the masses together or just the 50g mass.

Thank you very much, this was the right answer :)

 

[haruspex]

Thank you very much, this was the right answer :)

View attachment 338824

Good, but you show too many significant figures. The data you were given only have two (the 0.8s only one, but probably intends 0.80s). And you should always state the units. So better answers are 1.3 kg/s² and 0.021kg.