Georgepowell
- 179
- 0
I think it does... have I got that right?
If I have then why does it? is there a simple explanation?
If I have then why does it? is there a simple explanation?
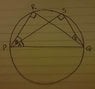
 would have been a lot better if i'd started off with a circle
would have been a lot better if i'd started off with a circle