- #1
Ryan187
- 5
- 1
Why the summation of the following function will be canceled out when we take the partial derivative with respect to the x_i?
Notice that x_i is the sub of (i), which is the same lower limit of the summation! Can someone, please explain in details?
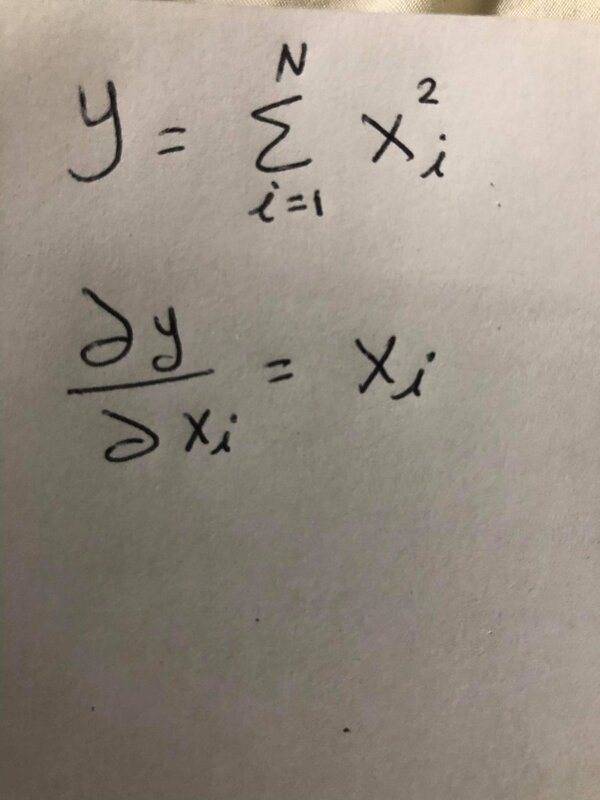
Notice that x_i is the sub of (i), which is the same lower limit of the summation! Can someone, please explain in details?