Why don't a charm-anticharm meson decay to pair of leptons?

[unscientific]

If you consider the $\chi_0$ with a mass of $3.4 GeV/c^2$ meson, why doesn't it decay to a pair of charged leptons? Technically it is possible though the weak interaction (Z boson) or EM interaction, right?

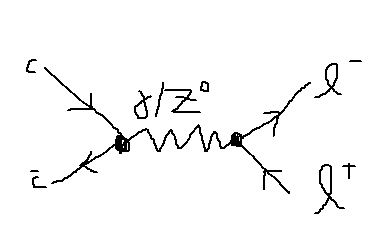
Is it because it is so heavily suppressed because the strong interactions are favoured? For example production of $D+D-$ mesons.

 

[fzero]

$\chi_{c,0}$ has angular momentum $J=0$ like the neutral pion, so at tree-level we can only have EM decays $\chi_{c,0}\rightarrow 2\gamma$ or $\chi_{c,0}\rightarrow \gamma \ell^+\ell^-$. So EM decays are suppressed by a factor of around 100 compared to the $J=1$ states.

 

[unscientific]

$\chi_{c,0}$ has angular momentum $J=0$ like the neutral pion, so at tree-level we can only have EM decays $\chi_{c,0}\rightarrow 2\gamma$ or $\chi_{c,0}\rightarrow \gamma \ell^+\ell^-$. So EM decays are suppressed by a factor of around 100 compared to the $J=1$ states.

Why can't weak decay via Z boson be possible?

Also even if $\chi$ decays electromagnetically, can't the photon couple to a pair of charged leptons?

What other $J=1$ states?

 

[fzero]

Why can't weak decay via Z boson be possible?

Also even if $\chi$ decays electromagnetically, can't the photon couple to a pair of charged leptons?

What other $J=1$ states?

The photon and Z boson are spin 1, and it is impossible to put a single spin 1 particle into a $J=0$ state. We need to conserve angular momentum at every step of the process, so we can't have a single photon or Z intermediate state anywhere in the decay process. The $J=1$ charmonium states can indeed decay via single photon or Z.

 

[unscientific]

The photon and Z boson are spin 1, and it is impossible to put a single spin 1 particle into a $J=0$ state. We need to conserve angular momentum at every step of the process, so we can't have a single photon or Z intermediate state anywhere in the decay process. The $J=1$ charmonium states can indeed decay via single photon or Z.

$\chi_{c0} = 0^{+}, \chi_{c1} = 1^{+}, \chi_{c2} = 2^{+}$. Ok, so the first can only decay electromagnetically and the rest can decay both via weak and EM interactions.

Even then, why can't the photon/Z boson decay to pairs of charged leptons?

 

[fzero]

$\chi_{c0} = 0^{+}, \chi_{c1} = 1^{+}, \chi_{c2} = 2^{+}$. Ok, so the first can only decay electromagnetically and the rest can decay both via weak and EM interactions.

Even then, why can't the photon/Z boson decay to pairs of charged leptons?

With a pair of spin 1/2 particles, it is possible to construct a $J=1$ angular momentum state. Like $\chi_{c1}$ and $\chi_{c2}$ we can also have some orbital angular momentum if necessary with a pair of particles. When there is a single particle in an intermediate state is when you are more likely to run into problems.

 

[unscientific]

With a pair of spin 1/2 particles, it is possible to construct a $J=1$ angular momentum state. Like $\chi_{c1}$ and $\chi_{c2}$ we can also have some orbital angular momentum if necessary with a pair of particles. When there is a single particle in an intermediate state is when you are more likely to run into problems.

That makes sense. But surely leptons are fermions as well, so they won't have the issue with spin. Why don't they decay to a pair of charged leptons then? Is it because strong interaction is preferred?

 

[fzero]

That makes sense. But surely leptons are fermions as well, so they won't have the issue with spin. Why don't they decay to a pair of charged leptons then? Is it because strong interaction is preferred?

The final $\ell^+\ell^-$ state can indeed have $J=0$, but the problem is that however we draw the diagram in your OP, there is always some reference frame in which we have a intermediate state consisting of a single spin 1 particle, which cannot be in a $J=0$ state. If we cooked some other diagram up to avoid this (like by adding a loop), then the additional interaction vertices we'd have to add would effectively suppress the process.

 

[unscientific]

The final $\ell^+\ell^-$ state can indeed have $J=0$, but the problem is that however we draw the diagram in your OP, there is always some reference frame in which we have a intermediate state consisting of a single spin 1 particle, which cannot be in a $J=0$ state. If we cooked some other diagram up to avoid this (like by adding a loop), then the additional interaction vertices we'd have to add would effectively suppress the process.

Sorry I didn't understand that at all. Based on the lowest order feynman diagram, I don't see why this following weak interaction is suppressed:

 

[RGevo]

The j psi resonance decays to charged leptons

http://en.m.wikipedia.org/wiki/J/psi_meson

 

[unscientific]

The j psi resonance decays to charged leptons

http://en.m.wikipedia.org/wiki/J/psi_meson

I know they do, but this isn't J/psi. This is $\chi_c$ meson. My question is why doesn't it decay to a pair of charged leptons, e.g. $\mu+\mu-$.

 

[RGevo]

Oops , sorry. I didn't read the text in any detail.

 

[mfb]

The graphical version of fzero's post.

 

[fzero]

Sorry I didn't understand that at all. Based on the lowest order feynman diagram, I don't see why this following weak interaction is suppressed:

It is necessary to conserve angular momentum at each vertex. The $\chi_{c0}$ is a 1P orbital state and has $J=0$. This implies that the $c$ and $\bar{c}$ spins are aligned. If the orbital angular momentum was zero, then $1/2 +1/2=1$ would work. However, $L=1$. If there was a second particle in the intermediate state then it would be possible for the vector + other particle system to have orbital angular momentum to make up the difference. However, we only have the vector and so cannot do so.

 

[mfb]

The decay is possible at tree-level with an intermediate Higgs boson (it has spin 0), but the contribution from this process is completely negligible.

 

[fzero]

The decay is possible at tree-level with an intermediate Higgs boson (it has spin 0), but the contribution from this process is completely negligible.

Yes, it's worth noting that, by comparing coupling constants, EM (radiative) decays tend to be suppressed by a factor of $10^{-4}$ with respect to strong decays. Weak decays are suppressed by more like 12 orders of magnitude compared to strong. There are a lot of other interesting effects in charm systems that can enhance some channels vs others, but the rarer the channel, the more likely it will be lost in the noise.

 

[Vanadium 50]

I'm sorry, but most of what has been written in this thread is simply incorrect.

The picture in #13 is not right. If it were true, the charged pion could never decay, since the pion is spin-0 but thge W is spin-1. Internal lines do not need to have the same spin as real particles.

The whole premise is also not right. The chi_0 probably does decay to lepton pairs. However, the partial width of this electromagnetic process is probably of order a few eV, and it competes with 10 MeV of other decays. So only one in a million - or a few million - chi_0's decay this way. The Higgs contribution to this is completely negligible.

Finally, the chi_0 is too light to decay into open charm.

 

[unscientific]

I'm sorry, but most of what has been written in this thread is simply incorrect.

The picture in #13 is not right. If it were true, the charged pion could never decay, since the pion is spin-0 but thge W is spin-1. Internal lines do not need to have the same spin as real particles.

The whole premise is also not right. The chi_0 probably does decay to lepton pairs. However, the partial width of this electromagnetic process is probably of order a few eV, and it competes with 10 MeV of other decays. So only one in a million - or a few million - chi_0's decay this way. The Higgs contribution to this is completely negligible.

Finally, the chi_0 is too light to decay into open charm.

So the strong interaction is preferred over the weak/EM interaction in this case?

 

[Vanadium 50]

By a factor of a million or so.

 

[fzero]

I'm sorry, but most of what has been written in this thread is simply incorrect.

The picture in #13 is not right. If it were true, the charged pion could never decay, since the pion is spin-0 but thge W is spin-1. Internal lines do not need to have the same spin as real particles.

The whole premise is also not right. The chi_0 probably does decay to lepton pairs. However, the partial width of this electromagnetic process is probably of order a few eV, and it competes with 10 MeV of other decays. So only one in a million - or a few million - chi_0's decay this way. The Higgs contribution to this is completely negligible.

Finally, the chi_0 is too light to decay into open charm.

The angular momentum discussion was a huge mistake, so many apologies to anyone misled and thank you for the correction.

The EM process is actually forbidden by C-parity conservation, which is in fact related to the angular momentum state. This is the same reason that $\pi^0\rightarrow \gamma^*\rightarrow e^+e^-$ doesn't occur. $\Gamma(\pi^0\rightarrow e^+e^-)/\Gamma_\mathrm{tot}$ is around $10^{-7}$ where you'd expect it to be via an intermediate Z.

 

[Vanadium 50]

The EM process is actually forbidden by C-parity conservation, which is in fact related to the angular momentum state.

Why? If L=0 and S=0 for the leptons, you have C even. The chi_0 has C even.

 

[fzero]

Why? If L=0 and S=0 for the leptons, you have C even. The chi_0 has C even.

Yes, but the photon has $C=-1$. The absence of single photon EM decays is how C-parity is inferred in practice.

 

[Vanadium 50]

But you can have two virtual photons.

 

[fzero]

But you can have two virtual photons.

Correct, but we had originally been talking about a tree level process and why it looked absent. The 1-loop process is roughly as rare as the tree-level weak process.

 

[Vanadium 50]

The tree level Z is going to be much rarer. The two-photon exchange is suppressed by alpha, 1/137, but the Z is suppressed by (m_chi/m_Z)⁴ or 1/500,000.

 

[fzero]

The tree level Z is going to be much rarer. The two-photon exchange is suppressed by alpha, 1/137, but the Z is suppressed by (m_chi/m_Z)⁴ or 1/500,000.

I think it's a bit more complicated than that:

$$\begin{split}
\Gamma(\pi^0\rightarrow 2\gamma) & \sim \alpha^2, \\
\Gamma(\pi^0\rightarrow 2\gamma^* \rightarrow e^+e^-) & \sim \alpha^4,\end{split}$$

but PDG has

$$ \frac{\Gamma(\pi^0\rightarrow e^+e^-)}{\Gamma(\pi^0\rightarrow 2\gamma)} \sim 6 \cdot 10^{-8}.$$

This is 3-4 orders of magnitude smaller than we'd expect from counting factors of $\alpha$, so there's some phase space or other numerical suppression going on too. The Z channel estimate is right in the ballpark of the observed value, so without an explicit calculation, we can't say which process is more likely.

 

[Vanadium 50]

Well, the pi0 is a pseudoscalar, so you need the electrons in a P-wave state, so you have a suppression because the wavefunction at the origin is zero. You don't have that problem with the chi_0.

 

[arivero]

A related question... if the spin of the intermediate particle does not matter, can it be also a gluino?

 

[Vanadium 50]

No, because the gluino has color charge. And it's not true that spin completely doesn't matter - you can't swap a fermion for a boson, for example.

 

[arivero]

No, because the gluino has color charge. And it's not true that spin completely doesn't matter - you can't swap a fermion for a boson, for example.

Well I was thinking in any of gluonic channels could be changed by "gluinoic" channels, as the color charge is in the same representation. The second point, I guess it translates to say that you can not have a vertex with a odd number of fermions, can you?