SUMMARY
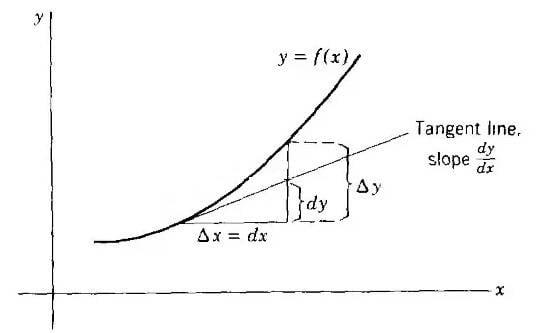
The discussion clarifies the distinction between Δy and dy in calculus, emphasizing that Δy represents the actual change in y, while dy denotes an infinitesimal change. It is established that Δy is not equal to dy, even for infinitesimally small dx, due to the linear approximation nature of dy. The conversation also critiques the notation of dy and dx, suggesting that they should be viewed as abbreviations rather than actual distances, and encourages a deeper understanding of derivatives through rigorous study.
PREREQUISITES
- Understanding of basic calculus concepts, specifically derivatives.
- Familiarity with the notation of limits, particularly
lim(Δx → 0) (Δy/Δx).
- Knowledge of the relationship between Δy and dy in the context of graphing functions.
- Awareness of different notations used in calculus, such as
y' and f'(x).
NEXT STEPS
- Study the concept of limits in calculus, focusing on
lim(Δx → 0) (Δy/Δx).
- Learn about the implications of using different notations in calculus, including
dy and y'.
- Explore the derivation and application of the chain rule in calculus.
- Read the series on derivatives linked in the discussion to gain a comprehensive understanding of the topic.
USEFUL FOR
Students of calculus, mathematics educators, and anyone seeking to clarify the concepts of derivatives and their notation in mathematical analysis.