- #1
Mike_bb
- 49
- 3
- TL;DR Summary
- Why is Delta y not equal to dy for infinitesimally dx on the graph?
Hello!
As is known, [itex]\Delta y = dy[/itex] for infinitesimally small [itex]dx[/itex]. It's true.
But if we have graph we may see that [itex]\Delta y[/itex] isn't equal to [itex]dy[/itex] even for infinitesimally small [itex]dx[/itex]. Why is that so?
Thanks!
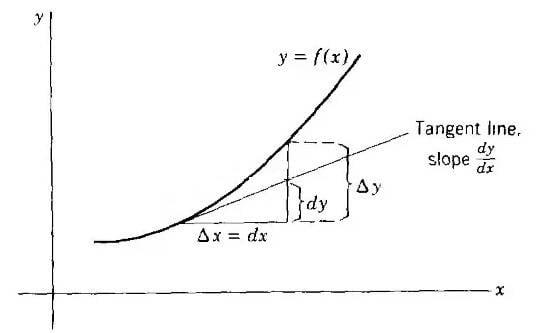
As is known, [itex]\Delta y = dy[/itex] for infinitesimally small [itex]dx[/itex]. It's true.
But if we have graph we may see that [itex]\Delta y[/itex] isn't equal to [itex]dy[/itex] even for infinitesimally small [itex]dx[/itex]. Why is that so?
Thanks!
Last edited: