Why is the angular momentum negative in a disk and stick collision?

[hhjjy]

Homework Statement

A 2.0-kg disk traveling at 3.0 m/s strikes a 1.0-kg stick of length 4.0 m that is lying flat on nearly frictionless ice as shown in the overhead view of Figure 11.12a. The disk strikes at the endpoint of the stick, at a distance r = 2.0 m from the stick’s center.

Assume the collision is elastic and the disk does not deviate from its original line of motion. Find the translational speed of the disk, the translational speed of the stick, and the angular speed of the stick after the collision. The moment of inertia of the stick about its center of mass is 1.33 kg m^2?

Relevant Equations

$L_{f} = L{i}$
$L = \vec{r} \times \vec{p}$
$|L| = mvr \sin{\theta}$

figure 11.12

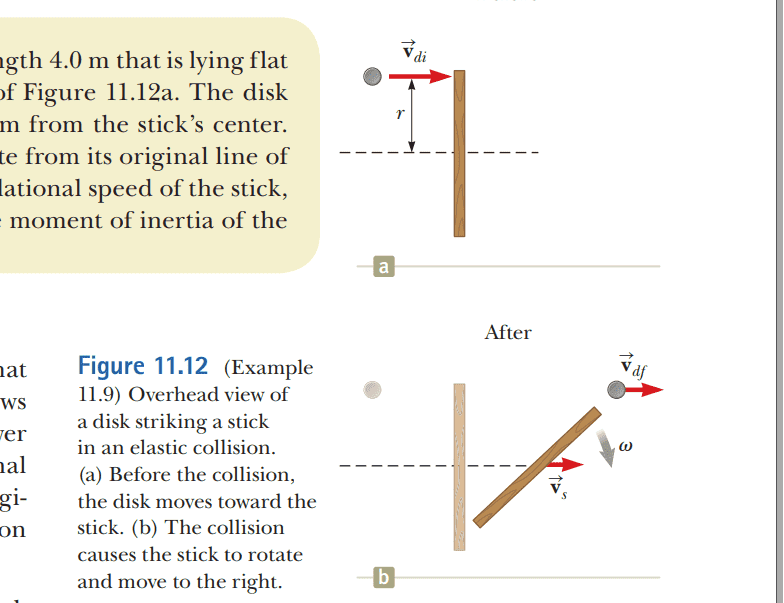
I need someone to explain why the angular momentum of the ball is $L_{f} = -rm_{d}V_{df} + I\omega$ rather than $L_{f} = rm_{d}V_{df} + I\omega$. How to distinguish the sign of the angular momentum?p.s. $\Delta\vec{L}_{total} = \vec{L}_{f} - \vec{L}_{i} = (-rm_{d}v_{df} + I\omega) - (-rm_{d}v_{di})$

 

[haruspex]

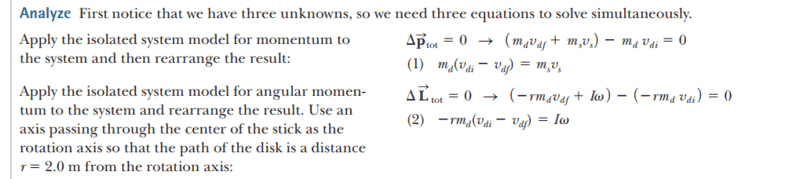
explain why the angular momentum of the ball is $L_{f} = -rm_{d}V_{df} + I\omega$ rather than $L_{f} = rm_{d}V_{df} + I\omega$. How to distinguish the sign of the angular momentum?

$L_{f} = -rm_{d}V_{df} + I\omega$ is the final angular momentum of ball plus stick. That of the ball is just $L_{f} = -rm_{d}V_{df}$
As is a common standard, the author is taking anticlockwise rotation as positive. What is misleading is that the diagram shows $\omega$ as being measured clockwise. To be correct, it should indicate the rotation as anticlockwise, but understanding that it will come out negative.

 

[hhjjy]

Ok, thanks.