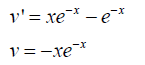Cadbury
- 11
- 0
View attachment 3778
So v' is the one to be integrated and v is the answer,
why is it not -xe^-x - e^-x ?
Thank you very much!
So v' is the one to be integrated and v is the answer,
why is it not -xe^-x - e^-x ?
Thank you very much!