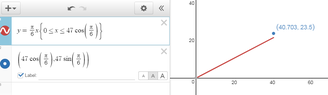
The discussion centers on the behavior of points on a graph in Desmos, specifically addressing why a point does not appear on the endpoint of a line. The mathematical expression $\frac{\pi}{6} \cdot 47 \cos(\frac{\pi}{6}) < 47 \sin(\frac{\pi}{6})$ is analyzed, leading to the conclusion that the slope, represented as $m = \frac{1}{\sqrt{3}}$, is not equal to $\frac{\pi}{6}$. This indicates a misunderstanding of the relationship between angles and slopes in the context of graphing.
PREREQUISITESStudents learning trigonometry, educators teaching graphing techniques, and anyone using Desmos for mathematical visualization.
