Amaelle
- 309
- 54
- Homework Statement
- look at the image
- Relevant Equations
- integrating impair function over symmetric region
Greetings
here is my integral
Compute the volume of the solid
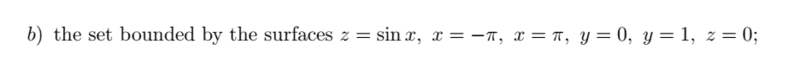
and here is the solution (that I don't agree with)

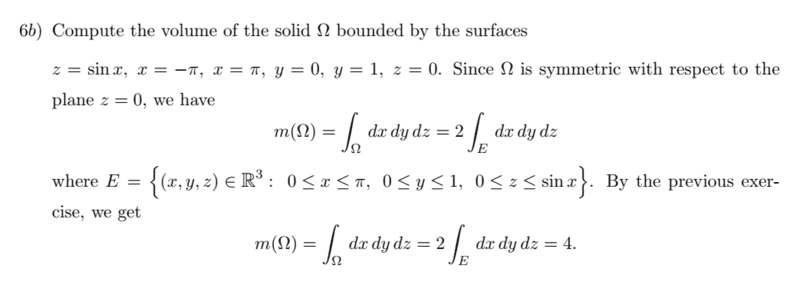
So as you can see they started integrating sinx from 0 to pi and then multiplied everything by two! for me sin(x) is an odd function and it's integral should be 0 over symmetric region!
thank you in advance!
here is my integral
Compute the volume of the solid
and here is the solution (that I don't agree with)
So as you can see they started integrating sinx from 0 to pi and then multiplied everything by two! for me sin(x) is an odd function and it's integral should be 0 over symmetric region!
thank you in advance!