Why (treating the two objects as a system) does not work here?

[Peter J]

Hello guys , i am really confused about this problem

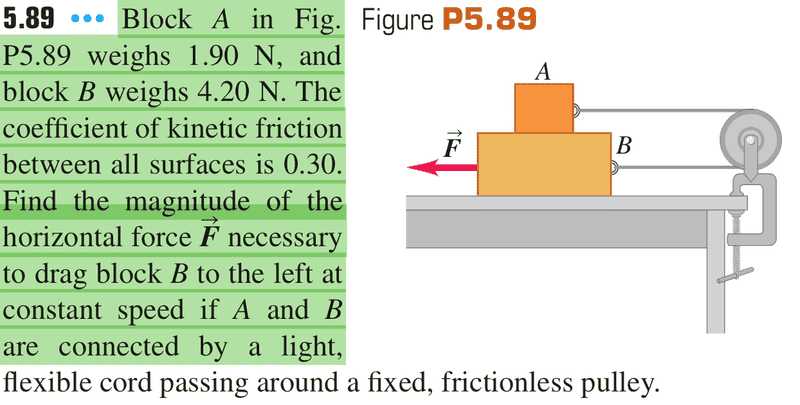
when i construct the free body diagram for each object individually , every thing goes fine and i can solve the problem and get the right solution,
BUT , as our professor said , we can consider two or more object as one system and apply Newtons law on it IF THEY HAVE THE SAME ACCELERATION , in this problem both have same acc , which is (0) .
but when i consider them is a system :

sum of external forces = m(total).a : a=0 >
sum of external forces=0 >
F-f (friction) =0
F=f(friction)
F=0.30 * 6.1 N = 1.83N Which is wrong ! the right answer is 3 N
-------
up to know , every problem that involved 2 or more objects with same acceleration i was able to solve it either way (consider all of them as a system and analyse the external forces , or by dividing them and study each object alone )
but this one does not seem to work for me .
-------
is there any thing wrong with eliminating the tension T from the equation of the composed system because it is an internal force ?

is there any thing wrong with eleminating the friction (A on B ) , ( B on A ) T from the equation of the composed system because it is an internal force ?

whats wrong !?

Thanks

 

[Bystander]

F=f(friction)

Okay.

F=0.30 * 6.1 N

"6.1?"

the right answer is 3 N

"3N ?"

 

[chingel]

If you view the two boxes as one system, the external forces are by the friction, by the force F and by the ropes attached to the boxes.

You can construct your system however you want, the acceleration of its center of mass is the total external force divided by the total mass. In your case, if you have ropes attached to your system of two boxes, of course you have to consider them because they are pulling your system.

 

[Peter J]

Okay.

"6.1?"

"3N ?"

6.1 is 4.2+1.9 : weight of A + weight of B .
yes the solution manual says 3N is the right answers

 

[Peter J]

If you view the two boxes as one system, the external forces are by the friction, by the force F and by the ropes attached to the boxes.

You can construct your system however you want, the acceleration of its center of mass is the total external force divided by the total mass. In your case, if you have ropes attached to your system of two boxes, of course you have to consider them because they are pulling your system.

the system is the two boxes with the rope , the external force ,as far as i know , is any force exerted by something outside the system ,
so the tension and the friction are internal forces which should not appear in Newton law , right ?

 

[Bystander]

is there any thing wrong with eleminating the friction (A on B ) , ( B on A )

Think this over,

6.1 is 4.2+1.9 : weight of A + weight of B .

and then rethink this.

 

[rcgldr]

I'm thinking that A opposes motion of B, and also adds to the weight of B, and the force has to overcome the tension used to move A, so the answer is force = .3(A + A + A + B) = 2.97N (not quite 3). If the masses were A = 1.93 N, B = 4.21 N or the coefficient of kinetic friction is 1/3.3, then the answer would be 3. To consider this as a system, you still have the same factors. friction of A on B, friction of A+B on the table, and tension in the cord.

 

[chingel]

the system is the two boxes with the rope , the external force ,as far as i know , is any force exerted by something outside the system ,
so the tension and the friction are internal forces which should not appear in Newton law , right ?

Yes, if you view the rope and the boxes as a single system (the part of friction that is between the boxes is an internal force). But then you have the pulley exerting a force on the rope (that is on your system, of which the rope is a part of), which you need to consider. If you wrap a rope around a pulley and pull on both ends of the rope, the pulley will feel a force and apply a force to the rope,

 

[Chestermiller]

the system is the two boxes with the rope , the external force ,as far as i know , is any force exerted by something outside the system ,
so the tension and the friction are internal forces which should not appear in Newton law , right ?

The friction force and the tension in the rope exerted on the two blocks are external forces to the system of two blocks. You have a force of 2T to the right that you haven't accounted for. Take your original force balances on each of the blocks and add them together, and then see what you get.

Chet

 

[Peter J]

thanks guys , just asked a friend of mine who is physics graduate and told me this story :
if we take the positive direction to be when the pull moves clockwise ,
then
for A we will have : +T - friction (B on A ) =0
for B we will have : -T - friction (A on B ) - friction (surface on A+B ) + F =0

if we add the two equations we will have " keeping in mind that friction (B on A ) = friction (A on B )"

- 2 friction (A on B ) - friction (surface on A+B ) + F = 0 >>
F = 2 friction (A on B ) + friction (surface on A ) " this will produce the a correct answer after substitution" .

now his point is ,, it is wrong to consider the 2 blocks with the rope a system because the internal forces don't cancel out , the tension cancel out but the friction (B on A ) and friction (A on B ) don't cancel , instead the add up because the both oppose the positive direction .

saying that , he concluded that in order to consider a composed object as system there must be two conditions :
1- the have the same acceleration
2- ALL of the internal forces cancel to each others

ANY COMMENT ? do you guys agree on that ?

 

[chingel]

You can consider any bodies you like as a system, nothing wrong with that. Just keep in mind that if the rope is part of the system, you have to consider the pulley, which pulls the rope with a force equal to twice the rope's tension. But to calculate the tension you have to go back to how the boxes will move, so it might not be really helpful.
By Newton's law the friction force felt by B due to A is exactly equal and opposite to the friction force to A by B. This applies to any two bodies, the forces applied to each other sum to 0, that is not the problem.

 

[Peter J]

By Newton's law the friction force felt by B due to A is exactly equal and opposite to the friction force to A by B. This applies to any two bodies, the forces applied to each other sum to 0, that is not the problem

but the sign convention is defined in a way that gives both of these forces a negative sign , they are opposite in direction relative to each other , but if we took the pulley clockwise rotation as our positive , then with respect to that both would have a negative sign. but I'm not even sure if that is possible ,,, i don't know , I'm just lost :)

 

[chingel]

If you view two bodies as one system then the forces between the bodies are internal forces. I don't know how to say it more clearly than that.

Probably the problem why you didn't get the correct answer is that you didn't consider the force from the pulley on the rope. It does not matter what bodies you view as a system, Newton's laws will still apply.

 

[Peter J]

If you view two bodies as one system then the forces between the bodies are internal forces. I don't know how to say it more clearly than that.

Probably the problem why you didn't get the correct answer is that you didn't consider the force from the pulley on the rope. It does not matter what bodies you view as a system, Newton's laws will still apply.

i totally see your point now , thanks , that was really helpful . :)

 

[Chestermiller]

thanks guys , just asked a friend of mine who is physics graduate and told me this story :
if we take the positive direction to be when the pull moves clockwise ,
then
for A we will have : +T - friction (B on A ) =0
for B we will have : -T - friction (A on B ) - friction (surface on A+B ) + F =0

if we add the two equations we will have " keeping in mind that friction (B on A ) = friction (A on B )"

- 2 friction (A on B ) - friction (surface on A+B ) + F = 0 >>
F = 2 friction (A on B ) + friction (surface on A ) " this will produce the a correct answer after substitution" .

now his point is ,, it is wrong to consider the 2 blocks with the rope a system because the internal forces don't cancel out , the tension cancel out but the friction (B on A ) and friction (A on B ) don't cancel , instead the add up because the both oppose the positive direction .

saying that , he concluded that in order to consider a composed object as system there must be two conditions :
1- the have the same acceleration
2- ALL of the internal forces cancel to each others

ANY COMMENT ? do you guys agree on that ?

I have a different perspective for you to consider. Here are your physics maven's force balance equations written in a slightly different manner, with forces directed to the left consistently positive and forces to the right consistently negative:

Mass B:
$$F-(W_A+W_B)\mu -W_A\mu -T=0$$

Mass A:
$$W_A\mu -T=0$$

If we subtract these two equations to eliminate the tension T, we obtain:
$$F-(W_A+3W_B)\mu=0$$
This gives the solution you correctly obtained:
$$F=(W_A+3W_B)\mu=2.97 N$$

Now, if we add the two force balance equations together, we get the force balance equation on the combination of the two masses:
$$F-(W_A+W_B)\mu -2T=0$$

In an earlier post in this thread, you were lamenting that the force balance on the combination of the two masses, which you wrote down as $F-(W_A+W_B)\mu=0$, did not give an answer consistent with your earlier result, which you knew to be the correct answer. I indicated that it did not give the correct answer because your force balance equation on the combined masses was incorrect. This is because it omitted the rope tensions. The rope tensions are external forces on the combination of the two masses, and must be included in their overall force balance. Since $T = W_A\mu$, the error in your earlier calculation was $2T = 2W_A\mu=1.14N$. If you add that to the 1.83N you obtained, you get 2.97 N (in agreement with your initial result).

Chet

 

[Peter J]

I have a different perspective for you to consider. Here are your physics maven's force balance equations written in a slightly different manner, with forces directed to the left consistently positive and forces to the right consistently negative:

that explanation is just amazing , i really really thank you , that was a clue ,
but one more thing :
what prevented me from thinking like that is what my friend said about pulleys
he said that our positive direction should always be according to the direction of the rotation of the pulley , according to that, the sign convention was :
for b , the forces that act to the right are positive and the forces that act to the left are negative ,
for a , the forces that act to the left are negative and the forces that act to the right are positive ,

and it did lead to a right answer ,

but from your solution i see that u did not follow that , is that wrong ? or its just another way ?

is it normal that you had the tension with the same sign on the two bodies ?

 

[chingel]

Nothing prevents you from doing that. Changing the sign convention from positive to negative for one body is exactly the same as multiplying the whole equation by -1, which doesn't change the result. He got the same equations, except one of them is multiplied by -1.

 

[Chestermiller]

that explanation is just amazing , i really really thank you , that was a clue ,
but one more thing :
what prevented me from thinking like that is what my friend said about pulleys
he said that our positive direction should always be according to the direction of the rotation of the pulley , according to that, the sign convention was :
for b , the forces that act to the right are positive and the forces that act to the left are negative ,
for a , the forces that act to the left are negative and the forces that act to the right are positive ,

and it did lead to a right answer ,

but from your solution i see that u did not follow that , is that wrong ? or its just another way ?

The way I did the problem is more conventional, but your friend's way is OK too. But, don't forget that force is a vector quantity, so in complicated problems, it is better to keep the direction of positive force consistent.

is it normal that you had the tension with the same sign on the two bodies ?

I just went by what the free body diagram told me.

Chet