Why Water Won't Flow From Faucet with 2000 Pa Pressure?

[Callmelucky]

Homework Statement

Can you please explain to me why is this the case? Thank you.

Relevant Equations

Hidrostatic pressure = gravitational constant * density * height

Picture below

can someone please explain me why will the water come out of faucet with the pressure of 2000 Pa?

I was expecting the answer to be "water will not come out thrugh the faucet because the pressure from the barrel is not strong enough to overcome the height of the pipe" since pressure depends only on height, gravitational constant and density of liquid, which is in this case water.

Thank you.

 

[erobz]

Homework Statement:: Can you please explain to me why is this the case? Thank you.
Relevant Equations:: Hidrostatic pressure = gravitational constant * density * height

Picture below

can someone please explain me why will the water come out of faucet with the pressure of 2000 Pa?

I was expecting the answer to be "water will not come out thrugh the faucet because the pressure from the barrel is not strong enough to overcome the height of the pipe" since pressure depends only on height, gravitational constant and density of liquid, which is in this case water.

Thank you.

As long as the pipe is full, the faucet is below the height of the water it will drain until the tank water drops by 20cm.

If the pipe is empty it’s not going to make it over the hump unless the tank is pressurized above atmospheric pressure.

 

[Callmelucky]

As long as the pipe is full, the faucet is below the height of the water it will drain until the tank water drops by 20cm.

If the pipe is empty it’s not going to make it over the hump unless the tank is pressurized above atmospheric pressure.

oohhh yeah, I didn't realise that pipe was full.
thank you.

 

[Merlin3189]

In the absence of atmospheric pressure, the water will come out of the faucet with initial pressure of 5000 Pa*. The water in the tank side of the pipe will stay where it is if the tank is sealed, or run back into the tank (which may overflow) until the pipe level matches the tank level.
This will happen so long as the atmospheric pressure is less than 3000 Pa, even if the pipe is initially filled (presumably by filling with pressurised water through the faucet.) Once atmospheric P exceeds 3 kPa, then siphonic action works.

*This is of course 0 Pa atmospheric pressure plus 5 kPa hydraulic.
If that sounds paradoxically larger than 2 kPa, the 2 kPa you give is relative to atmospheric pressure, so the absolute pressure at the faucet is 102 kPa - as it needs to be to push its way out against the surrounding 100 kPa air.

 

[erobz]

I guess I really didn't think into it too much, but in the initial state shown the tank must be sealed, and under greater than atmospheric pressure at the upper surface. Given a sealed tank I don't think the siphon action could work. I don't believe much of anything would come out of that faucet for any extended period of time. How much that would come out would be dependent on how much the barrel expanded from its original volume given a static head of 30 cm (assuming the water itself is virtually incompressible). I doubt that is any significant volume.

 

[Merlin3189]

Quite so. Just considering the possibilities.
Once I talked about zero air pressure, the water won't stay in the top of the tube, unless the faucet is shut and tank sealed. So after you've somehow forced the water in and closed all exits, you start the expt by opening one or both ends.

My main idea was that water can't support tension. People often talk as if the lower end of a siphon pulls water down, but it really just allows the air pressure on the higher level to push the water up over the hill, by pushing down against the air pressure on the lower level. No air pressure = no siphon.

 

[hutchphd]

My main idea was that water can't support tension. People often talk as if the lower end of a siphon pulls water down, but it really just allows the air pressure on the higher level to push the water up over the hill, by pushing down against the air pressure on the lower level. No air pressure = no siphon.

Water (partially via surface tension) can certainly "suck" This is how a closed tube manometer works. It is both incompressible and, in a confining geometry, inextensible. So I disagree with this assertion. But it will dissolve gas and cavitate at a low enough pressure.

 

[Merlin3189]

Water (partially via surface tension) can certainly "suck" This is how a closed tube manometer works. It is both incompressible and, in a confining geometry, inextensible. So I disagree with this assertion. But it will dissolve gas and cavitate at a low enough pressure.

Agree there is a small amount of cohesion, but I'd have thought negligible in the context of water tank and pipes. (But I'll be interested to know how much: I haven't attempted a calculation myself. )

If a closed tube manometer is what I think, then I disagree. The gas pressure from the open end or experimental end, pushes the liquid up into the evacuated sealed tube. No external pressure, no liquid rise.

A mercury barometer used to be made with a sealed tube filled with Hg. When inverted into a pool of Hg, the liquid would completely empty out if there were no air pressure pushing it up the tube. It doesn't matter how long the tube is and how much Hg is in to start with, the Hg only rises as far as the air pressure will push it.

Cavitation is interesting. The water is under some pressure from its own weight, again pushing the liquid together, though it obviously does cohere to some degree. Do bubbles that form from dissolved gases count as cavitation? Do they redissolve quickly as pressure increases? I think cavitation is about the formation of water vapour bubbles when the surface pressure is below the svp, and the significance is the sudden collapse as the pressure rises again - but I'm definitely not particularly informed on this topic.

 

[erobz]

In an open top tank a siphon is created by priming the line, then bringing the end of the line below the tank water surface. There is no pressure difference between the tank water surface and the discharge of the line, they are both at atmospheric.

 

[hutchphd]

Do bubbles that form from dissolved gases count as cavitation?

Not usually considered as cavitation. The cavitation is essentially caused by water being at a low enough pressure locally (usually because of turbulent flow) that the water boils making a cavity.
For our problem: The vapor pressure of water at 100C is 14.7psi. At 20C the water vapor pressure is 0.2psi. So if you suck on it harder than -14.5psi gauge pressure at room temperature it will boil . That cavitation is what limits a lift pump to 28 ft. But the efficacy of the siphon is from this suction (so long as you do not get to the vapor pressure of the liquid). The useful suction is restricted by vapor pressure.

 

[Merlin3189]

In an open top tank ... There is no pressure difference between the tank water surface and the discharge of the line, they are both at atmospheric.

The air pressures may be the same, but presumably the liquid pressures differ, else why would the water come out?
Thanks for the comment on water svp.
My conclusion from that is, the siphon will "break" when the pressure at the top of the link is 0.2 psi - so when the water height gives hydraulic pressure 0.2 psi less than atmospheric (about 1.4% less.) So you'd be better off with a liquid that had zero, or lowest, svp and no dissolved gases. They serve merely to push back against atmospheric pressure pushing the liquid upwards.
Or perhaps not, if they lower the density of the liquid? One way of pumping water over a barrier is to blow air bubbles into the ascending pipe, so that the water level in that pipe is higher than in the source, and simply let it overflow the barrier. There may be a kinetic element at work here, but this tries to improve on the static mechanism.

IMO it still comes down to the more dense liquid pushing the less dense mixture, rather than anything sucking.
But I think I'm digressing, as usual on PF, so maybe we better leave it there?

 

[erobz]

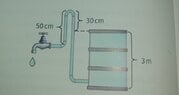
IMO:

The entire contents of the dashed box are under vacuum if flow is established with some velocity $v$.

Start by applying the "Energy Equation" between positions 1 and 2 (under the assumption of steady flow - not time varying). 1 is the free water surface, and 2 is located inside the pipe at the free water surface. The tank is assumed to larger that the pipe. It doesn't have to be, but it makes the result more obvious.

$$ \frac{P_1}{\gamma} + z_1 + \frac{v_1^2}{2g} = \frac{P_2}{\gamma} + z_2 + \frac{v_2^2}{2g} + \sum_{1 \to 2} k \frac{v_i^2}{2g} $$

$P_1$ is 0 gage

$1$ is the elevation datum $z_1 = z_2 = 0 \rm{elev.}$

The tank is assumed large as such $v_1 \approx 0$

The last term is a generic head loss term for any real (viscous flow) it is always positive for any established flow in the system.

By continuity (constant pipe diameter) $v_2 = v_i = v$

We find that the pressure inside the pipe at $2$ is given by:

$$ \boxed{ \frac{P_2}{\gamma} = - \left( \frac{v^2}{2g} + \sum_{1 \to 2} k \frac{v^2}{2g} \right) }$$

Thus, the pressure at $2$ is necessarily at vacuum (and is it atmospheric just below it).

We can do the same analysis for $2 \to 3$:

$$ \boxed{ \frac{P_3}{\gamma} = \frac{P_2}{\gamma} - \left( z_3 + \sum_{2 \to 3} k \frac{v^2}{2g} \right) } $$

It should be apparent that $P_3$ is the peak vacuum pressure in the system. Also, $3$ has a limit, as the pipe rises higher and higher, the pressure $P_3$ is approaching the vaporization pressure of the liquid. Cavitation will occur at some maximum elevation for the siphon at $z_3$ and the flow will be interrupted as the bubbles expand.

The vacuum is created by the adhesion @hutchphd is pointing out. You are priming the siphon with vacuum conditions, then water must "fall out" pulling on the water next to it to maintain those vacuum conditions once "manual suction" is removed.

The air pressures may be the same, but presumably the liquid pressures differ, else why would the water come out?

The pressure at the surface $1$ and the fluid jet are the same almost immediately after the jet exits the pipe. The pressure change propagates at the speed of sound in the fluid.

 

[hutchphd]

then water must "fall out" pulling on the water next to it to maintain those vacuum conditions once "manual suction" is removed.

And of course the static absolute pressure at the top elbow of box (3) in drawing cannot go below the 0.2psi vapor pressure of water. This limits the max height z of the elbow to ~28ft for water at room temperature.

 

[erobz]

And of course the static absolute pressure at the top elbow of box (3) in drawing cannot go below the 0.2psi vapor pressure of water. This limits the max height z of the elbow to ~28ft for water at room temperature.

Yeah, I was implying that (without verified calculation) with this statement:

It should be apparent that P3 is the peak vacuum pressure in the system. Also, 3 has a limit, as the pipe rises higher and higher, the pressure P3 is approaching the vaporization pressure of the liquid. Cavitation will occur at some maximum elevation for the siphon at z3 and the flow will be interrupted as the bubbles expand.

using those equations its some negative gage pressure...but talking absolute pressures, sure.

 

[Merlin3189]

.... its some negative gage pressure...but talking absolute pressures, sure.

Perhaps this is the key. Negative gauge pressure stays greater (less negative) than -1 bar (negative 1 atmosphere pressure.)
"... P3 is the PEAK vacuum pressure ..." confused me, but I guess you meant the minimum pressure: to me, pressure is the opposite of vacuum. I'm not accustomed to negative pressures, though I can see it may be useful to use that idea sometimes.
P3 is always less than P1 and P2, so the water is always being pushed by higher pressure towards a lower pressure.

If we got rid of the water - by using a liquid with zero SVP (??) or separating it from the vacuum with a piston say - it wouldn't matter how far negative you sucked the pipe, you could never suck up the piston beyond the height it was pushed by atmospheric pressure. OTOH if the pipe has a vacuum in it and the water has risen to the appropriate height for the atmospheric pressure, then it can always be pushed higher by increasing atmospheric pressure. And that will be true whether or not the faucet is open to the same higher atmospheric pressure.

 

[erobz]

Perhaps this is the key. Negative gauge pressure stays greater (less negative) than -1 bar (negative 1 atmosphere pressure.)
"... P3 is the PEAK vacuum pressure ..." confused me, but I guess you meant the minimum pressure: to me, pressure is the opposite of vacuum. I'm not accustomed to negative pressures, though I can see it may be useful to use that idea sometimes.
P3 is always less than P1 and P2, so the water is always being pushed by higher pressure towards a lower pressure.

Fluids Mechanics in the engineering discipline typically works with gage pressures.

Yes, I meant point $3$ would have the highest vacuum pressure i.e. maximal negative gage pressure or minimal absolute pressure in the system.