psycovic23
- 47
- 0
Homework Statement
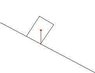
A tall uniform rectangular block sits on an inclined plane. If Us = .4, does the block slide or fall over as the angle is slowly increased? Also, the block is 3a units tall and "a" units wide.
The Attempt at a Solution
Just by intuition, I figured that it would tip over, since the static friction is pretty high, but I'm not sure how to prove that.
I initially thought you could say that as the incline increased, the force between the bottom of the block and the incline plane would increase, creating torque on the block. But in this case, there's no opposing torque at the top of the block, so by this logic, it would tip over as soon as there was any incline. Any help would be appreciated. Thanks!