mcastillo356
Gold Member
- 658
- 361
- TL;DR
- Texbook don't seem to regard on the range and domains of function product. A search on the net gives clues, but I'd wish some more learning.
Hi, PF
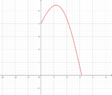
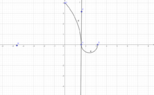
I only have a clue on the topic I present; the answer involves the ##\subset##, maybe ##\subseteq## concepts; I mean that the only answer I've obtained is that both range and domain of the product of two functions are the inclusion of both. I include a picture regarding the example of the textbook, which shows to functions between ##0## and ##\pi##.
Greetings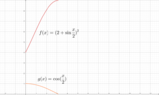
I only have a clue on the topic I present; the answer involves the ##\subset##, maybe ##\subseteq## concepts; I mean that the only answer I've obtained is that both range and domain of the product of two functions are the inclusion of both. I include a picture regarding the example of the textbook, which shows to functions between ##0## and ##\pi##.
Greetings