Writing the correct diff. equations for an RC circuit

[Yoni V]

Homework Statement

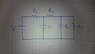
Given the circuit in the picture, I need to:
a. write a system of diff. equations that could solve the charges on each cap. and current on each resistor, and write them in a vector/matrix form.
b. solve the equations for t>>τ

Homework Equations

Kirchoff's laws, perhaps Thevenin's theorem, although this wasn't my attempt at it.

The Attempt at a Solution

I wrote the equations for voltage loops.
First was the outer loop, yielding
$V=I_{1}R_{1}+I_{2}R_{2}+I_{3}R_{3}=I_{1}R_{1}+\frac{1}{2}I_{1}R_{2}+\frac{1}{4}I_{1}R_{3}=R_{1}\dot{Q_{1}}+R_{2}\dot{Q_{2}}+I_{3}R_{3}$
Second was
$V=R_{1}\dot{Q_{1}}+R_{2}\dot{Q_{2}}+Q_{2}/C_{2}$
Third was
$V=R_{1}\dot{Q}_{1}+Q_{1}/C_{1}+Q_{2}/C_{2}$
And lastly, although obviously one of these is redundant, the loop containing both capacitors yields
$I_{2}R_{2}=R_{2}\dot{Q}_{2}=Q_{2}/C_{2}-Q_{1}/C_{1}\Rightarrow Q_{2}/C_{2}=Q_{1}/C_{1}+R_{2}\dot{Q_{2}}$

I think I'm supposed to have enough info here to be able to write a decent set of diff. equations, but somehow meshing the equations together didn't result in anything. I mean, first I'm not sure if the equations are indeed enough for a theoretical solution, and second I'm a little puzzled at how to transform all of this into vector form.

Any leads?

Thanks!

Edit: Trying to force an answer from this resulted in:
$\begin{bmatrix}\dot{Q_{1}}\\ \dot{Q_{2}} \end{bmatrix}=\begin{bmatrix}\frac{-1}{R_{1}C_{1}} & \frac{-1}{R_{1}C_{2}}\\ \frac{-1}{R_{2}C_{1}} & \frac{1}{R_{2}C_{2}} \end{bmatrix}\begin{bmatrix}Q_{1}\\ Q_{2} \end{bmatrix}+\begin{bmatrix}\frac{V}{R_{1}}\\ 0 \end{bmatrix}$

And then for part b, it results (as for all other equation combos) that Q1=Q2=0 (equating the derivatives to 0). This doesn't make much sense to me, but I can't figure out what's wrong.

 

[Hesch]

I don't think that your equations are correct. They look like Kirchhoffs voltage law, but I don't understand what you are doing. How come that I₂ = ½*I₁ and that I₃ = 1/4*I₁?

You must read Kirchhoffs voltage law, and sketch the current loops that you use as for I1, I2, I3.

Edit: I assume that you switch on the battery at t = 0 ?

 

[Yoni V]

OH Yes!
You're right.. my thinking was that the currents are additive, and therefore split at the junctions, but of course they don't necessarily split evenly...
Ok, I'll have another go at it.
Thanks

 

[Yoni V]

Still not working.
These are the equations I came up with this time.
I₀ is the current going out directly from the voltage source.
I₁ is the current reaching C1, I₂ is the current reaching C2.
Now, using Kirchoff's laws correctly (I think...), we get for the resistors:
R1 gets current I₀, R2 gets I₁-I₀, R3 gets I₀+I₂-I₁.
And for voltage loops we get:
1. Outer loop: $V=I_{0}R_{1}+\left(I_{1}-I_{0}\right)R_{2}+\left(I_{0}+I_{2}-I_{1}\right)R_{3}=\left(R_{1}-R_{2}+R_{3}\right)I_{0}+\left(R_{2}-R_{3}\right)I_{1}+R_{3}I_{2}$
2. Loop through V and C2: $V=I_{0}R_{1}+\left(I_{1}-I_{0}\right)R_{2}+Q_{2}/C_{2}=\left(R_{1}-R_{2}\right)I_{0}+R_{1}I_{1}+\frac{Q_{2}}{C_{2}}$
3. Loop through V and C1: $V=I_{0}R_{1}+Q_{1}/C_{1}$
4. Loop through C1 and C2: $Q_{1}/C_{1}=R_{2}I_{1}-R_{2}I_{0}+Q_{2}/C_{2}$
5. Loop through C2 and R3: $Q_{2}/C_{2}=R_{3}I_{0}+R_{3}I_{2}-R_{3}I_{1}$
6. Loop through C1 and R3: $Q_{1}/C_{1}=\left(I_{1}-I_{0}\right)R_{2}+\left(I_{0}+I_{2}-I_{1}\right)R_{3}$

That's it. The last eq. is redundant, but it's a nice validation for the rest of the equations.
Isolating I₀ from loop equation no. 3 we get $I_{0}=\frac{V}{R_{1}}-\frac{Q_{1}}{R_{1}C_{1}}$
Finally, combining equations 1,2,4,5 into the final system after substituting I₀, I ended up with
$\begin{bmatrix}R_{2}-R_{3} & R_{1}R_{3}\\ R_{1}^{2} & 0\\ R_{1}R_{2} & 0\\ R_{1}R_{3} & -R_{1}R_{3} \end{bmatrix}\begin{bmatrix}\dot{Q_{1}}\\ \dot{Q_{2}} \end{bmatrix}+\begin{bmatrix}\frac{R_{2}-R_{1}-R_{3}}{C_{1}} & 0\\ \frac{R_{2}-R_{1}}{C_{1}} & \frac{R_{1}}{C_{2}}\\ \frac{R_{2}-R_{1}}{C_{1}} & \frac{R_{1}}{C_{2}}\\ \frac{R_{3}}{C_{1}} & \frac{R_{1}}{C_{2}} \end{bmatrix}\begin{bmatrix}Q_{1}\\ Q_{2} \end{bmatrix}=\begin{bmatrix}\left(R_{2}-R_{3}\right)V\\ R_{2}V\\ R_{2}V\\ R_{3}V \end{bmatrix}$

That's incorrect, and I want to know whether it's just due to a minor algebraic error on the way, or whether I again misused Kirchhoff's laws.
I equated the derivatives to 0 to solve for the steady state solution, and after solving Q1 and Q2 in terms of the constants, substituting them in the leftover equations resulted in a dependency between the constants (rather than purely a true statement).

Thanks again

 

[theodoros.mihos]

Try to write equations for $\dot{V}$ to use Kirchhoff's laws. With $\dot{Q}$ the voltage expression is not clear.

 

[Yoni V]

Hmm.. but the voltage I think is given as a constant

 

[theodoros.mihos]

When use 2nd law we right the current for the whole hang and express the i.e. $I_{c1}$ as $I_1-I_2$. With this notation relations for current can written as:
$$ I_1 = \frac{V_0-Q_1/C_1}{R_1} ,\, I_2 = \frac{Q_1/C_1-Q_2/C_2}{R_2} ,\, I_3 = \frac{Q_2/C_2}{R_3} $$
I think this notation makes easier equations.

 

[Hesch]

I1 is the current reaching C1, I2 is the current reaching C2.

( Just an example ).

I2 is not "reaching" anything: It's a circulation current, spinning around in the loop.

You must read Kirchhoffs voltage law, and sketch the current loops that you use as for I1, I2, I3.

Kirchhoffs law states:

∑ ΔV = 0 , as for a circulation path in a circuit.

You must sketch these (3) circulation paths ( ending up with 3 equations ). Example:

( you could call the red current, m1, and the blue current, m2. Having found m1 and m2, the current through the center resistor becomes m1 + m2. )

I'd express the impdances of a capacitor, C, as Zc = 1 / sC. Then

I = dQ/dt could be expressed as I(s) = Q*s. Then your matrix system could be expressed by Laplace transform instead of by the time-domain. But I don't know if you are familiar with Laplace transform?

( You may also use Kirchhoffs current law instead, ending up with only 2 equations. Using KCL you find the voltages. By using KVL you find the currents. But when knowing the voltages/currents, currents/voltages are easily found by Ohms law ).

 

[Yoni V]

Perhaps I am misusing terms, as English is not mother tongue, but indeed I didn't mean to say the current is "going" anywhere.
Thing is, I don't understand what is wrong with my equations.

Ok... I got it, I think.. Just stupid algebra mistakes...

 

[Hesch]

Perhaps I am misusing terms, as English is not mother tongue, but indeed I didn't mean to say the current is "going" anywhere.

Don't be sorry for that: I'm from Denmark, having the same "problem".

Just you understand, that KVL is calculating with circulation currents, which are rarely physical currents. You solve the physical current by adding the loop-currents, found with a few equations. Many people mix up these loop-currents and physical currents, ending up with the double number of equations.

So set up 3 equations ( as for your problem ), add the loop-currents and you have found the physical currents.

 

[Yoni V]

So maybe I didn't understand it after all, as I'm not familiar with circulation loops.
From what I've learned, I can notate the currents on a circuit like in the following figure (and I could also add bigger loop eqs., but they cancel out eventually)

 

[vela]

Those equations look good. Now solve for $I_0$, $I_1$, and $I_2$ in terms of V, Q1, and Q2.

 

[Hesch]

#11: You are mixing physical currents and loop-currents.

The green arrows are not just paths. They are loop-currents. Call them m1, m2, m3. I0, I1, I2 are physical currents, you can measure them. Z1 = 1/sC₁ and so on.

Here it goes:

(m1): V - m1*R1 - 1/(sC₁)*(m1-m2) = 0
(m2): 1/(sC₁)*(m1-m2) - m2*R2 + 1/(sC₂)*(m3-m2) = 0
(m3): Try it yourself

Solve m1, m2, m3, then:

I₀ = m1
I₁ = m1 - m2
I₂ = m2 - m3

 

[vela]

Just you understand, that KVL is calculating with circulation currents, which are rarely physical currents.

KVL has nothing to do with currents. KVL says if you sum the voltage differences around any closed loop, they'll sum to 0. That's all it says.

When you use mesh analysis (which is only one possible way to solve the problem), you typically apply KVL to the loops that each mesh current travels. It's not necessary to use those loops, however.

 

[Hesch]

KVL says if you sum the voltage differences around any closed loop, they'll sum to 0. That's all it says.

Well, you are free to make the substitution:

V = I * R

With KCL you are free to use:

I = V / R

 

[Yoni V]

Ok, I finally made it, thank you all for you help and patience!