carllacan
- 272
- 3
Hi.
Has anybody here any experience with SciPy? I'm trying to get SciPy to adjust a gaussian function to some data. For more details its the photopeak of Co60. This is what I do:
The result is not what I would expect, though, though:
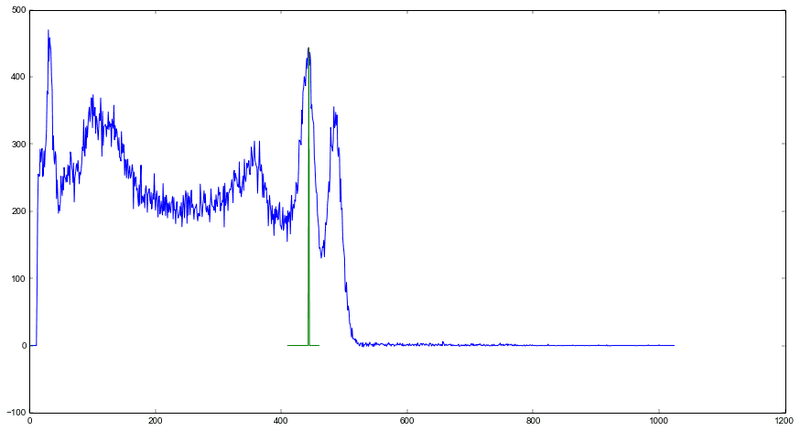
The green line is my fit, the blue one the original data. The gaussian should b much wider!
What am I doing wrong?
Thank you for your time.
Has anybody here any experience with SciPy? I'm trying to get SciPy to adjust a gaussian function to some data. For more details its the photopeak of Co60. This is what I do:
Code:
import numpy as np
from scipy.optimize import curve_fit
# counts is a numpy array which holds the number of counts for each channel
# start is the position in the count array where the peak starts, and
# end is the position where the peak ends, both guesstimated by eye
# define the gaussian function
gauss = lambda x, u, v: (1 / (v*np.sqrt(2*np.pi)) * np.exp(-(x-u)**2/(2*v**2)))
# create the space over which the gaussian should be fitted
x = np.linspace(start, end, end - start)
# the initial parameters, estimated from the start and end positions
a0 =[ (start + end)/2, (end - start)/(4*np.log(2))]
# fit the gaussian function over the interval x to the datapoints counts[data:end]
fit = curve_fit(f, x, counts[start:end], a0)
mean = fit[0][0]
var = fit[0][1]The result is not what I would expect, though, though:
The green line is my fit, the blue one the original data. The gaussian should b much wider!
What am I doing wrong?
Thank you for your time.