Wrongly applying Faraday's Law to time changing loops

[MisterX]

Faraday's law is
$$\nabla \times \mathbf{E} = - \frac{d\mathbf{B}}{dt} $$
If we let our time dependent surface be $\Sigma(t)$ and its boundary $\partial \Sigma(t)$, then by Stokes' theorem
$$ \oint_{\partial \Sigma(t)} \mathbf{E} \cdot d\boldsymbol{\ell} = - \int_{\Sigma(t)} \frac{\partial \mathbf{B}}{\partial t} \cdot d\mathbf{A}$$
The crucial thing to notice is that in general
$$\int_{\Sigma(t)} \frac{\partial \mathbf{B}}{\partial t} \cdot d\mathbf{A} \neq \frac{d}{dt} \int_{\Sigma(t)} \mathbf{B}\cdot d\mathbf{A} $$
You cannot take the time derivative out of the integral when the boundary of the integral changes in time. So when the loop changes in time,
$$ \oint_{\partial \Sigma(t)} \mathbf{E} \cdot d\boldsymbol{\ell} \neq \frac{d\Phi}{dt}$$

Yet, I have repeatedly seen introductory physics students being expected to use Faraday's law for time changing loops. One type of relevant problem is the bar on a rail problem¹.

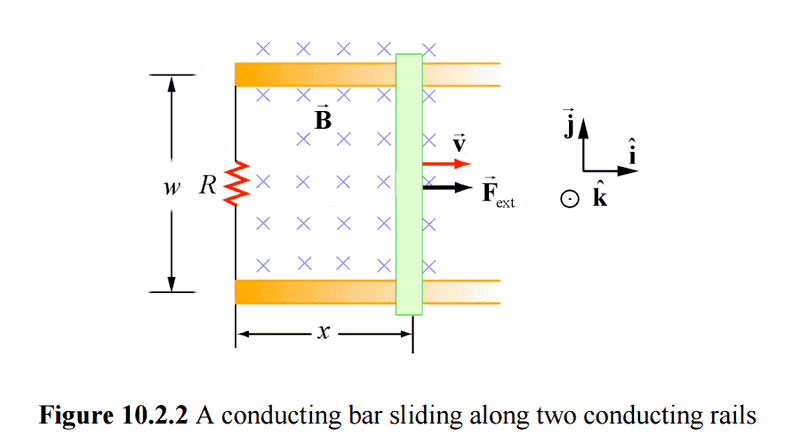
The correct interpretation is that magnetic forces on the electrons in the bar lead to a buildup of electric charge that supports a flow of current. Note that the charges produce a conservative electric field. Contrast this with the non-conservative electric field produced by Faraday's law. It is wrong to teach these as two equivalent approaches, because they are conceptually different. It is arguably mere coincidence that they might sometimes produce the same result for the current. As an aside, if we say the bar has some resistance, the matter is further complicated because we can no longer use the argument that $\mathbf{E} = 0$ in the bar to have equilibrium. I mention this because I have seen problems given to students that involve the moving portions of loops having resistance.

If you happen to be involved in teaching introductory physics, I encourage you to consider not asking questions that lead the students to use Faraday's law in these situations where it doesn't really apply. If any of you have an argument why we can generalize the concept of emf being related to change in flux to include the potential due to static charge buildup in moving loops in a way that is always correct, I might like to see that argument.
1 Figure resused from from MIT under Creative Commons License

 

[Geofleur]

There is a discussion here that seems relevant: http://physics.stackexchange.com/questions/61851/faradays-law-for-a-current-loop-being-deformed

One of the posters shows that the time derivative can be taken outside the integral sign as long as a correction term is added.

 

[cabraham]

This question was on my Ph.D. qualifier exam, which I passed. Faraday's law is applicable here, no reason to think otherwise. The key to understanding this problem is the integrand "B⋅dA". Although B is fixed in value, "A" is varying. As the bar slides along the rails, the area of the enclosed loop increases linearly with the bar's displacement. Since B⋅dA is non-zero, there is an E field with curl (non-conservative). The loop being conductive results in a current, which results in another magnetic field which opposes the original mag field per law of Lenz. The ratio of loop voltage open circuited and loop current is the loop impedance which consists of the self inductance of the loop added to the loop resistance in quadrature. This is similar to a squirrel cage rotor induction motor, where a time varying flux is present in the area of a low resistance loop.

I will elaborate if needed.

Claude