unknown_2
- 28
- 0
Hey, I'm having some difficulty calculating couple moment. i understand that \sumM = \sumFd. here's an example:
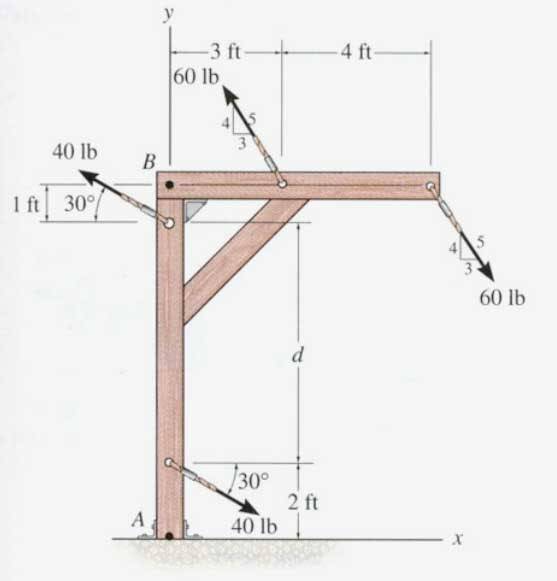
it asks to resolve the couple forces.
the answer is:
(4/5)(60lb) = 48lb
and
(40lb)(cos30)
\sumM = -(48lb)(4ft) + (40lb)(cos30)(8ft)
Now, i don't understand why "-(48lb)(4ft)" is negative. I'm not sure when to use a negative value. Can someone explain this to me?
Cheers
it asks to resolve the couple forces.
the answer is:
(4/5)(60lb) = 48lb
and
(40lb)(cos30)
\sumM = -(48lb)(4ft) + (40lb)(cos30)(8ft)
Now, i don't understand why "-(48lb)(4ft)" is negative. I'm not sure when to use a negative value. Can someone explain this to me?
Cheers