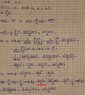Pzi
- 26
- 0
This applies to natural numbers n and N where n<N.
We have N balls representing numbers 1,2,...,N.
We randomly choose n of those balls which happen to represent numbers {k_1},{k_2},...,{k_n}.
We then define a random variable X = {k_1} + {k_2} + ... + {k_n}.
What is the mean and variation of X?
Well there are \left( {\begin{array}{*{20}{c}}N\\n\end{array}} \right) equally likely combinations and every one of them brings n summands. So we get \left( {\begin{array}{*{20}{c}}<br /> N\\<br /> n<br /> \end{array}} \right) \cdot n summands overall. Since there is no bias towards any particular number it means that every number is added \left( {\begin{array}{*{20}{c}}<br /> N\\<br /> n<br /> \end{array}} \right) \cdot \frac{n}{N} times hence our mean:
E\left( X \right) = \frac{{\left( {\begin{array}{*{20}{c}}<br /> N\\<br /> n<br /> \end{array}} \right) \cdot \frac{n}{N} \cdot \left( {1 + 2 + ... + N} \right)}}{{\left( {\begin{array}{*{20}{c}}<br /> N\\<br /> n<br /> \end{array}} \right)}} = \frac{n}{N} \cdot \frac{{N\left( {N + 1} \right)}}{2} = \frac{{n\left( {N + 1} \right)}}{2}.
Unfortunately variance seems to be an entirely different animal since I cannot just rip sums apart and add numbers in a different order. Any ideas?
We have N balls representing numbers 1,2,...,N.
We randomly choose n of those balls which happen to represent numbers {k_1},{k_2},...,{k_n}.
We then define a random variable X = {k_1} + {k_2} + ... + {k_n}.
What is the mean and variation of X?
Well there are \left( {\begin{array}{*{20}{c}}N\\n\end{array}} \right) equally likely combinations and every one of them brings n summands. So we get \left( {\begin{array}{*{20}{c}}<br /> N\\<br /> n<br /> \end{array}} \right) \cdot n summands overall. Since there is no bias towards any particular number it means that every number is added \left( {\begin{array}{*{20}{c}}<br /> N\\<br /> n<br /> \end{array}} \right) \cdot \frac{n}{N} times hence our mean:
E\left( X \right) = \frac{{\left( {\begin{array}{*{20}{c}}<br /> N\\<br /> n<br /> \end{array}} \right) \cdot \frac{n}{N} \cdot \left( {1 + 2 + ... + N} \right)}}{{\left( {\begin{array}{*{20}{c}}<br /> N\\<br /> n<br /> \end{array}} \right)}} = \frac{n}{N} \cdot \frac{{N\left( {N + 1} \right)}}{2} = \frac{{n\left( {N + 1} \right)}}{2}.
Unfortunately variance seems to be an entirely different animal since I cannot just rip sums apart and add numbers in a different order. Any ideas?
Last edited: