- #1
ChaseRLewis
- 43
- 0
So been self-studying till this point and it has been pretty easy / generic with the PDE's. At this point though the math gets a bit more out of my depth and was curious if someone might lend a hand in helping me understand what is going on.
My question is pretty much is there a good algorithm to solve for the constants given the situation below. To solve this problem it requires an iterative method to find the constants for the wave function that meets the requirements based on the potential.
given n = 1 you get
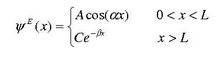
giving you the following solution for the constants alpha and beta
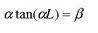
each constant having the value of
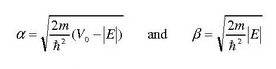
so to solve for the energy (and thus the wave equation) for an arbitrary potential value
you must solve for the constants that satisfies the potential value. (This is called an Eigenvector right?)
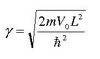
the L2 is because they transformed the alpha and beta values to unitless dimensions (these are pics from a website I'm using to supplement my understanding : P easier than typing all this).
 TL:DR; Longwinded, question to basically ask is there a good marching algorithm to solve this type of problem for the given constants? Google isn't giving me much, at this point unfortunately.
TL:DR; Longwinded, question to basically ask is there a good marching algorithm to solve this type of problem for the given constants? Google isn't giving me much, at this point unfortunately.
My question is pretty much is there a good algorithm to solve for the constants given the situation below. To solve this problem it requires an iterative method to find the constants for the wave function that meets the requirements based on the potential.
given n = 1 you get
giving you the following solution for the constants alpha and beta
each constant having the value of
so to solve for the energy (and thus the wave equation) for an arbitrary potential value
you must solve for the constants that satisfies the potential value. (This is called an Eigenvector right?)
the L2 is because they transformed the alpha and beta values to unitless dimensions (these are pics from a website I'm using to supplement my understanding : P easier than typing all this).