Troubleshooting Ln: Tips to Improve Sleep

[Focus]

I've had troubled sleep because of this...

I tryed a lot and got this...

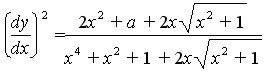
Can you spot any mistakes or give me hints on how to approach this
Thanks

 

[SebastianG]

That is an equation that shows the "complex variable" version of arcsinh (x) as equal to the integral version of it (on real values). Like a definition. You obtain the first with the complex functions sinhz and some algebra, and the second one with a trigonometric substitution (or using mathematica, hehe)

 

[Focus]

That is an equation that shows the "complex variable" version of arcsinh (x) as equal to the integral version of it (on real values). Like a definition. You obtain the first with the complex functions sinhz and some algebra, and the second one with a trigonometric substitution (or using mathematica, hehe)

I am so confused...I know that the second one can be obtained by using y=arsinh(x) but I can't get the log of the function to differentiate to that

 

[HallsofIvy]

It helps a lot if you write it clearly! I think you mean that IF
y= ln\left[x+ (1+x^2)^{\frac{1}{2}}\right]
then
(1+x^2)\left(\frac{dy}{dx}\right)^2= 1
which is the same as saying that
\frac{dy}{dx}= \frac{1}{(1+x^2)^{\frac{1}{2}}}

 

[Focus]

It helps a lot if you write it clearly! I think you mean that IF
y= ln\left[x+ (1+x^2)^{\frac{1}{2}}\right]
then
(1+x^2)\left(\frac{dy}{dx}\right)^2= 1
which is the same as saying that
\frac{dy}{dx}= \frac{1}{(1+x^2)^{\frac{1}{2}}}

The problem is I can't derive \frac{dy}{dx}= \frac{1}{(1+x^2)^{\frac{1}{2}}} from y= ln\left[x+ (1+x^2)^{\frac{1}{2}}\right]...
I can only derive it from y=arsinh(x)

 

[NateTG]

The problem is I can't derive \frac{dy}{dx}= \frac{1}{(1+x^2)^{\frac{1}{2}}} from y= ln\left[x+ (1+x^2)^{\frac{1}{2}}\right]...
I can only derive it from y=arsinh(x)

It seems like it pops right out from the chain rule.

 

[HallsofIvy]

Yep.
y= ln\left[x+ (1+x^2)^{\frac{1}{2}}\right]so
y'= \frac{1}{x+(1+x^2)^{\frac{1}{2}}}\left(1+(\frac{1}{2})(1+ x^2)^{-\frac{1}{2}}(2x)\right)\)
Now factor that
(1+ x^2)^{-\frac{1}{2}}
out of the numerator and every thing else cancels!

 

[Focus]

Hmmm...I tried that but I'll do it again, cheers for the help