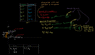- #1
Nickg140143
- 30
- 0
Homework Statement
A student stands on the edge of a cliff and throws a stone horizontally over the edge with a speed "v1". The cliff is "h" meters high. Given [h,v1], Determine:
a. The time to hit the ground
b. The horizontal distance traveled
c. The magnitude and direction of the stone's velocity just before hitting the ground
Homework Equations
x direction
[tex]
V_x=V_{0x}
[/tex]
[tex]
x=V_0\cos{\theta}
[/tex]
y direction
[tex]
V_y=V_{0y}-gt
[/tex]
[tex]
y=V_{0y}t-\frac{1}{2}gt^2
[/tex]
[tex]
V_y^2=V_{0y}^2-2gy
[/tex]
The Attempt at a Solution
If I set up my coordinate system so that 0 is ground level, and h is cliff level (where the stone was thrown from), and the distance to the landing point of the stone when it hits the ground is, say "r" meters from 0 in the x direction.
I've shown what work I have in the attached images, but to be perfectly honest, I'm having trouble with the entire basic strategy to approaching this problem.
When I try to solve for x distance r, I need time. So when I try to solve for time, that becomes reliant on r. I can't even think of anything else I can find.
I feel I'm either not utilizing the possible angles within this problem, or I've completely missed some fundamental idea in regards to projectile motion.
A good shove in the right direction on this kind of problem would be VERY much appreciated.