tsslaporte
- 12
- 0
Homework Statement
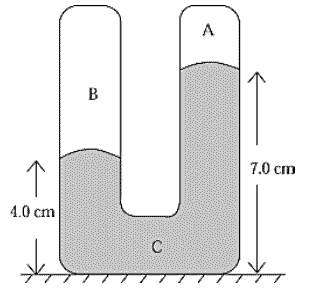
The U-tube in the figure is sealed at both ends. It contains a gas in A, another gas in B, and mercury in C. The heights of the mercury in the two arms are as shown. The density of mercury is 13.6 g/cm3. If the pressure in A is 1 × 10^4 dyn/cm2, the pressure in B is
The attempt at a solution
4-7 = 3CM
0.03m * 9.81 * 13600 kg/m^3 which = 4000 Pa which converts to 4x10^4 dyn/cm^2
But the answer given was 5x10^4 dyn/cm^2
I am not sure what I am doing wrong?
Edit: 4x10E4 is the pressure difference. So I have to add A which is 1x10E4 and that gives B = 5x10E4.
Could someone explain why I add A?
The U-tube in the figure is sealed at both ends. It contains a gas in A, another gas in B, and mercury in C. The heights of the mercury in the two arms are as shown. The density of mercury is 13.6 g/cm3. If the pressure in A is 1 × 10^4 dyn/cm2, the pressure in B is
The attempt at a solution
4-7 = 3CM
0.03m * 9.81 * 13600 kg/m^3 which = 4000 Pa which converts to 4x10^4 dyn/cm^2
But the answer given was 5x10^4 dyn/cm^2
I am not sure what I am doing wrong?
Edit: 4x10E4 is the pressure difference. So I have to add A which is 1x10E4 and that gives B = 5x10E4.
Could someone explain why I add A?
Last edited: