- #1
diethaltao
- 14
- 0
Homework Statement
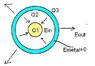
A solid insulating sphere of radius a = 5.6 cm is fixed at the origin of a co-ordinate system as shown. The sphere is uniformly charged with a charge density ρ = -159 μC/m3. Concentric with the sphere is an uncharged spherical conducting shell of inner radius b = 10.7 cm, and outer radius c = 12.7 cm.
A charge Q = 0.0724μC is now added to the conducting shell. What is V(a), the electric potential at the outer surface of the insulating sphere, now? Define the potential to be zero at infinity.
Homework Equations
E = kQ/(r^2)
Q = ρV
The Attempt at a Solution
I know that if the 0.0724μC was not present, the electric potential at the outer surface of the insulating sphere would be:
-kQ((1/b)-(1/c)) + (kQ/a) (*equation 1)
Using Q = ρV = -1.1696x10^-7 C.
But now that the spherical conducting shell has charged, I'm confused. Letting
0.0724μC = Q
-0.11696μC = q
I've tried:
((Q+q)/(4πεo))*(1/c) + (q/(4πεo))*((1/b)-(1-c)) + (q/(4πεo))*(1/a)
but this is wrong and I'm not sure why. I've also tried taking my answer from *equation 1 and adding that to (Q/4πεo)*(1/c) or (Q/4πεo)*(1/b) and it is still wrong.
Thanks in advance!