A string over a pulley with two hoops wound like spools on each end

[pleasantresult]

Homework Statement

This is question 1.3 from Fetter and Walecka.

A massless string is placed over a massless pulley, and each end is wound around and fastened to a vertical hoop. The hoops have masses M1, M2 and radii R1, R2. The apparatus is placed in a uniform gravitational field g and released with each end of the string aligned along the field. Show that the tension in the string is tau = g*M1*M2*(M1+M2)^(-1).

Relevant Equations

tau = g*M1*M2*(M1+M2)^(-1)

I have seen the solution to this problem but I don't understand it.

Here is my drawing of the problem.

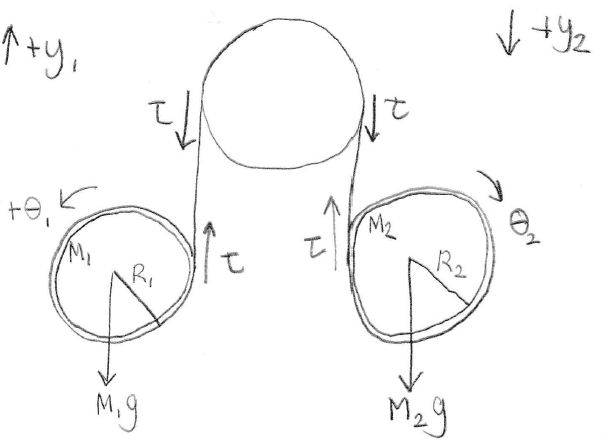
Apparently I should do the sum of the forces and sum of the torques for both hoops like this:
hoop 1:
(1) τ - M₁g = M₁(a_1t-a_1R)
(2) τR₁ = ½M₁R₁²a_1r/R₁
hoop 2:
(3) M₂g - τ = M₂(a_1t+a_2r)
(4) τR₂ = ½M₂R₂²a_2r/R₂
Where a_1t and a_2t are the translation accelerations up or down of hoops 1 and 2.
Where a_1r and a_2r are the rotational tangential accelerations of hoop 1 and hoop 2.
In the sum of the forces equations, the total linear accelerations are found by subtracting the tangential rotational acceleration for hoop 1 and adding the tangential rotational acceleration for hoop 2 based on the chosen orientations of positive linear and angular directions for the hoops.
In the third equation, you can sub in a_1t where you would expect a_2t because without rotation, the distance that hoop 2 drops will be the same as the distance that hoop 1 rises.
Then you have four equations with the four unknowns τ, a_1t, a_1r, and a_2r which you can solve to get the result that τ = gM₁M₂/(M₁+M₂)^-1
Everything about this setup makes sense to me except the moments of inertia that are used in equations 2 and 4. Isn't the moment of inertia of a thin hoop about its center MR² not ½MR²?

 

[haruspex]

(1) τ - M₁g = M₁(a_1t-a_1R)
Where a_1t and a_2t are the translation accelerations up or down of hoops 1 and 2.
Where a_1r and a_2r are the rotational tangential accelerations of hoop 1 and hoop 2.

Are you sure about eqn 1? On the left you have the net upward force on the hoop. Why should the right hand side not just be M₁a_1t? Do you perhaps intend that a_1t is a relative acceleration?
And it is too vague to say the accelerations are "up or down". You need to say which (i.e. which way is to be taken as positive) or it is not possible to know what the signs should be in the equations.

 

[Lnewqban]

... Isn't the moment of inertia of a thin hoop about its center MR² not ½MR²?

http://hyperphysics.phy-astr.gsu.edu/hbase/ihoop.html

 

[pleasantresult]

Thank you for your response.

Are you sure about eqn 1? On the left you have the net upward force on the hoop. Why should the right hand side not just be M₁a_1t? Do you perhaps intend that a_1t is a relative acceleration?

I am sure about equation 1 because I have seen the solution and these four equations can be solved together to determine the correct expression for τ. I thought it made sense that the actual acceleration of the hoop would be the difference between the acceleration due to being pulled and the tangential acceleration of rotating back down. But I see your point and I'm not sure why this equation is justified. Would relative accelerations explain it like you suggested?

And it is too vague to say the accelerations are "up or down". You need to say which (i.e. which way is to be taken as positive) or it is not possible to know what the signs should be in the equations.

I tried to indicate the positive directions. I put that the position for hoop 1, y₁, is positive pointing up. Then the acceleration would also be positive pointing up. I put that the position for hoop 2, y₂, is positive pointing down. Then the acceleration would also be positive pointing down. And I used θ₁ and θ₂ to indicate the positive rotational directions for hoops 1 and 2.

Do you have any thoughts about the moment of inertia of a thin hoop? Why would the solution have it as ½MR² and not MR²?

 

[pleasantresult]

http://hyperphysics.phy-astr.gsu.edu/hbase/ihoop.html

Thank you for your response.

So why does the solution I have seen for this problem look like it uses ½MR²? I don't think it makes sense to apply the parallel axis theorem in this situation. The hoops are rotating about their centers right? And applying the parallel axis theorem can only make the moment of inertia bigger than its moment about center.

 

[haruspex]

Thank you for your response.

So why does the solution I have seen for this problem look like it uses ½MR²? I don't think it makes sense to apply the parallel axis theorem in this situation. The hoops are rotating about their centers right? And applying the parallel axis theorem can only make the moment of inertia bigger than its moment about center.

I dropped the spurious a_xR terms from equations 1 and 3, and used MR² instead of half that. Remarkably, I got the target expression for $\tau$. So it looks like a case of two errors cancelling.

 

[pleasantresult]

I dropped the spurious a_xR terms from equations 1 and 3, and used MR² instead of half that. Remarkably, I got the target expression for $\tau$. So it looks like a case of two errors cancelling.

Thank you.

Great! I'm going to try that because that would make more sense to me, too.

 

[etotheipi]

Are you sure about eqn 1? On the left you have the net upward force on the hoop. Why should the right hand side not just be M₁a_1t? Do you perhaps intend that a_1t is a relative acceleration?

I am sure about equation 1 because I have seen the solution and these four equations can be solved together to determine the correct expression for τ.

@haruspex is right, if $a_{1t}$ is the acceleration of the centre of mass of the hoop in the lab frame then $T - M_1 g = M_1 a_{1t}$. This is an application of one of Euler's Laws of Motion.

You can denote the velocity of the part of the disk currently just in contact with the string (taking $\hat{y}$ pointing upward) as $v = r_1 \omega_1 - v_1$. It follows that $a = r_1 \alpha_1 - a_1$ and you can do the same for the second mass.

The key part is to understand how the two accelerations are related!

 

[etotheipi]

(1) τ - M₁g = M₁(a_1t-a_1R)

The only context in which this relation would make sense would if if $a_{1t}$ were the acceleration of the edge of the disk w.r.t. the lab frame. But that doesn't appear to be how you've defined it.

 

[Lnewqban]

Thank you for your response.

So why does the solution I have seen for this problem look like it uses ½MR²? I don't think it makes sense to apply the parallel axis theorem in this situation. The hoops are rotating about their centers right? And applying the parallel axis theorem can only make the moment of inertia bigger than its moment about center.

I have no idea, and I am not sure about the solution, but it is an interesting situation.
This problem combines an Atwood machine with two spinning falling rings of different masses and radii (two yo-yo's basically).

https://en.wikipedia.org/wiki/Atwood_machine

https://physics.stackexchange.com/questions/518729/simple-yo-yo-work-problem

The solution would be simpler if the rings were statically (not spinning) hanging from the string, just like regular masses do in this type of problems.
Then the string would be moving with certain acceleration proportional to the difference between the masses only.

The radii and the two angular accelerations introduce additional complication.
It seems to me that tension of the string should be lower with spinning rings than with non-spinning bodies of equivalent masses.