Angularly Propagating Modes In a Cylindrical Waveguide

[Twigg]

Hey all,

I was citing a result from a review paper in my paper, and I think it's wrong. I would really appreciate an outside perspective if anyone has the time!

The result was for the electric field outside a metal rod (cylindrical waveguide, if you prefer) in vacuum. Here's the picture (you can ignore the $k_e$ and $k_\gamma$ in the diagram, that's unrelated):

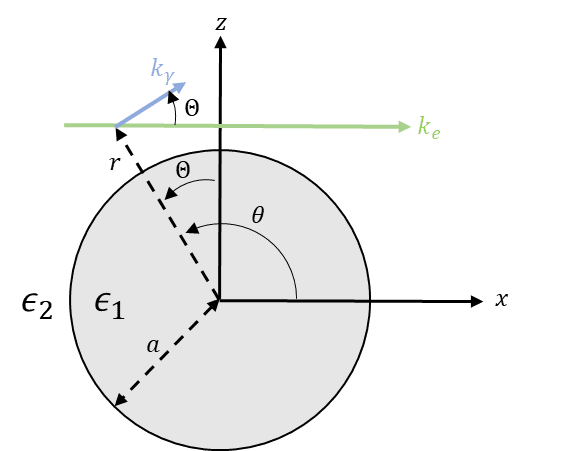
So, the result is for the electric field for r > a. And this is specifically for waves propagating around the circumference of the cylinder, not down the axis (so the wavevector $\vec{k}$ points along $\hat{\theta}$, NOT along $\hat{z}$).

The result the paper gives is this: $$E_r = \frac{-\beta}{kr} H_\beta(kr) e^{i(\beta \theta - \omega t)}$$ $$E_\theta = i H_\beta '(kr) e^{i(\beta \theta - \omega t)}$$ where $k = \sqrt{\epsilon_2} \frac{\omega}{c}$ and $H_{\beta}$ are the Hankel functions of the first kind (Hankels of the first kind are chosen because they give retarded waves, while the 2nd kind gives advanced waves).

This solution doesn't seem right to me. I don't think it's even a solution of the wave equation, because the angular frequency and the radial frequencies don't match up. To prove this hunch, I did a little mathematica script to check if this solution solves the Helmholtz equation:

b = 2;
f[r_, \[Theta]_, z_] := (b/(k*r))*BesselJ[b, k*r]*Exp[I*b*\[Theta]];
(* f[r_,\[Theta]_,z_] := BesselJ[b,k*r]*Exp[\[ImaginaryI]*b*\[Theta]]; *) (*This is a test case!*)
(Laplacian[f[r, \[Theta], z], {r, \[Theta], z}, "Cylindrical"] + k^2 * f[r, \[Theta], z]) // FullSimplify

And the result is (for $\beta = 2$ as a test case):

Which is not zero!

As a sanity check, I tried the same code for a function I know solves Helmholtz's equation:

Am I right to think this solution is fishy? Or have I finally gone off the deep end?Where I got this from:
These solutions come from page 11 of this open-access review. The review cites a giant E&M textbook called "Electromagnetic Theory" by J. A. Stratton, which has a whole, massive chapter on cylindrical waveguides (Chapter VI). I'm still sifting through it, it's really dense. I'm posting here because I may run out of time before I find the answer on my own.

 

[Twigg]

Welp, this one's going to be a self-solved thread. I'm wrong, the review paper is right. I found another reference that backs up the review paper. It's another textbook, this one on polariton modes. I need to still figure out what I was doing wrong when I checked it against the Helmholtz equation. These solutions seem to come out of the Hansen vector fields generated by a scalar wavefunction, so they should be rock solid. I'll post if I find a coherent answer.

 

[Twigg]

Yep! Issue resolved. The trick is that I'm dumb and I took the scalar Laplacian of the $\theta$ component of the electric field, when the vector Laplacian is *not* the same as the scalar Laplacian of the cylindrical components

Tl;dr:
$$ [\nabla^2 + k^2] \vec{E} = 0 \not \rightarrow [\nabla^2 + k^2] E_\theta = 0$$

Whoops!

 

[vanhees71]

That's a trap everybody gets caught in once ;-).

 

[ergospherical]

Yes for example consider a simpler example like $\boldsymbol{F} = f(r) \boldsymbol{e}_{\theta}$, then \begin{align*}

\nabla^2 \boldsymbol{F} &= \nabla(\nabla \cdot \boldsymbol{F}) - \nabla \times (\nabla \times \boldsymbol{F}) \\

&= \nabla(f \nabla \cdot \boldsymbol{e}_{\theta} + \boldsymbol{e}_{\theta} \cdot \nabla f) - \nabla \times (f \nabla \times \boldsymbol{e}_{\theta} + \nabla f \times \boldsymbol{e}_{\theta})

\end{align*}Since $\nabla f = \boldsymbol{e}_{r} \partial_{r} f$, it follows from the orthogonality of the basis that $\boldsymbol{e}_{\theta} \cdot \nabla f = 0$. Furthermore,\begin{align*}

\nabla \times \boldsymbol{e}_{\theta} &= \dfrac{1}{r} \boldsymbol{e}_{z} \\

\mathrm{and} \ \ \ \nabla \cdot \boldsymbol{e}_{\theta} &= 0

\end{align*}so it follows that\begin{align*}

\nabla^2 \boldsymbol{F} &= -\nabla \times \left(\left( \dfrac{f}{r} + \partial_{r} f \right) \boldsymbol{e}_{z}\right) \\

&= \boldsymbol{e}_{\theta} \dfrac{\partial}{\partial r} \left( \dfrac{f}{r} + \partial_{r} f\right) \\

&= \boldsymbol{e}_{\theta} \left( -\dfrac{f}{r^2} + \dfrac{1}{r} \partial_{r} f + \partial_{r}^2 f\right)

\end{align*}So $(\nabla^2 \boldsymbol{F})_{\theta} = -\dfrac{f}{r^2} + \dfrac{1}{r} \partial_{r} f + \partial_{r}^2 f$. On the other hand, \begin{align*}

\nabla^2 F_{\theta} = \nabla^2 f = \dfrac{1}{r} \partial_{r} \left( r \partial_{r} f\right) = \dfrac{1}{r} \partial_{r} f + \partial_{r}^2 f \neq (\nabla^2 \boldsymbol{F})_{\theta}

\end{align*}

 

[Twigg]

That's a trap everybody gets caught in once ;-).

It's the "once" part that gets me