- #1
stolencookie
Homework Statement
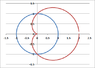
r=1 and r=1+cos(theta), use a double integral to find the area inside the circle r=1 and outside the cardioid r=1+cos(theta)
Homework Equations
The Attempt at a Solution
I am confused on the wording and how to set it up. I tried setting it up by setting theta 0 to pi. and r as 1 to 1+cos(theta). I used r drd(theta) as the equation to use.