- #1
KedarMhaswade
- 35
- 6
- TL;DR Summary
- Must the axes of the 2-d coordinate system used in vector resolution be perpendicular to each other?
Hello,
This question is with regards to the discussion around page 56 (1971 Edition) in Anthony French's Newtonian Mechanics. He is discussing the choice of a coordinate system where the axes are not necessarily perpendicular to each other. Here is the summary of what I read (as applied to vectors in a two-dimensional plane):
Vector A makes the angles α and β with two coordinate axes (we'll still call the axes ##x-##axis and ##y-##axis respectively) not necessarily perpendicular to each other (i.e. α+β is not necessarily π/2). Then, ##A_x = A\cdot\cos\alpha## and ##A_y=A\cdot\cos\beta##, where ##A_x, A_y## are the magnitudes of the ##x, y##-components of ##\vec{A}## respectively. In the generalized two-dimensional case, we have the relationship ##\cos^2\alpha+\cos^2\beta = 1##.
I have redrawn the accompanying figure:
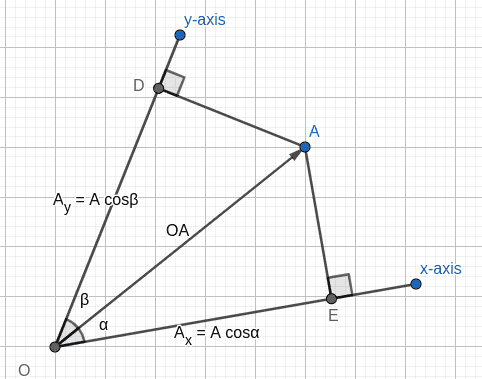
How does French arrive at the *generalized* relationship: ##\cos^2\alpha+\cos^2\beta = 1## in two dimensions and ##\cos^2\alpha+\cos^2\beta+\cos^2\gamma = 1## in three dimensions? Am I misreading the text, or summarizing it wrong (sorry, you need the book to ascertain that)?
In the case of perpendicular axes in two dimensions, it is clear why it would hold, since ##\alpha+\beta=\frac{\pi}{2}##. But I am not sure how it holds in general.
This question is with regards to the discussion around page 56 (1971 Edition) in Anthony French's Newtonian Mechanics. He is discussing the choice of a coordinate system where the axes are not necessarily perpendicular to each other. Here is the summary of what I read (as applied to vectors in a two-dimensional plane):
Vector A makes the angles α and β with two coordinate axes (we'll still call the axes ##x-##axis and ##y-##axis respectively) not necessarily perpendicular to each other (i.e. α+β is not necessarily π/2). Then, ##A_x = A\cdot\cos\alpha## and ##A_y=A\cdot\cos\beta##, where ##A_x, A_y## are the magnitudes of the ##x, y##-components of ##\vec{A}## respectively. In the generalized two-dimensional case, we have the relationship ##\cos^2\alpha+\cos^2\beta = 1##.
I have redrawn the accompanying figure:
How does French arrive at the *generalized* relationship: ##\cos^2\alpha+\cos^2\beta = 1## in two dimensions and ##\cos^2\alpha+\cos^2\beta+\cos^2\gamma = 1## in three dimensions? Am I misreading the text, or summarizing it wrong (sorry, you need the book to ascertain that)?
In the case of perpendicular axes in two dimensions, it is clear why it would hold, since ##\alpha+\beta=\frac{\pi}{2}##. But I am not sure how it holds in general.