- #1
faen
- 140
- 0
Below are a couple of problems given, 3 and 4. They are about drawing bode plots based on a given transfer function. I am wondering if anybody could please let me know if I drew the Bode plots right or wrong? Also I am not sure about how to find the crossover frequency. On task 3 I calculated it to be 6.18 by solving a second degree equation. However, the graph I found crosses the x-axis (frequency axis) at w = 10. I'd be thankful if anybody could help finding out which one of those solutions are wrong and why. Thanks a lot :)
3. The transfer function W0 of the open loop is
(see corresponding picture below)
Draw the a(w)dB asymptotic magnitude plot, mark K and draw the j (w )
exact phase plot. Based on the plots, determine the crossover frequency c w
and phase margin t
j .
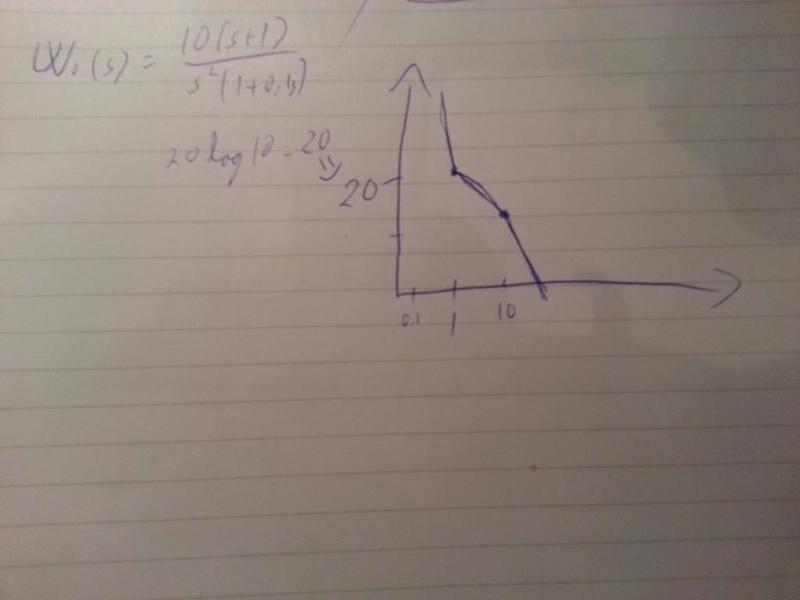
4. The transfer function W0 of the open loop is
(see picture below)
Draw the a(w)dB asymptotic magnitude plot, mark K and determine the
crossover frequency c w . Hint: What is the value of 2 K /w in case ofw = 1?
The crossover frequency wc is the frequency where the absolute value of the transfer function equals to one. It is also where the graph crosses the x-axis (frequency axis). Is this right?
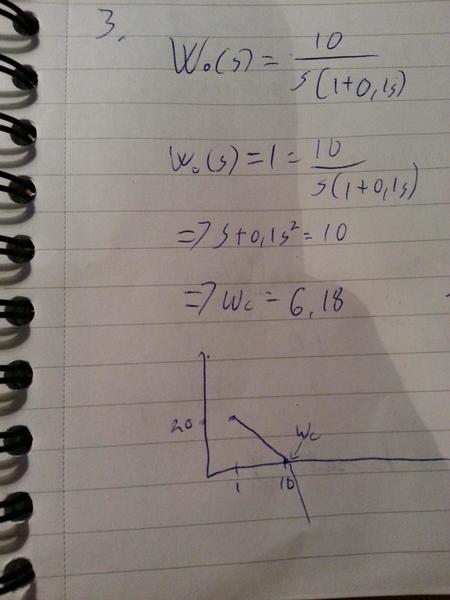
Homework Statement
3. The transfer function W0 of the open loop is
(see corresponding picture below)
Draw the a(w)dB asymptotic magnitude plot, mark K and draw the j (w )
exact phase plot. Based on the plots, determine the crossover frequency c w
and phase margin t
j .
4. The transfer function W0 of the open loop is
(see picture below)
Draw the a(w)dB asymptotic magnitude plot, mark K and determine the
crossover frequency c w . Hint: What is the value of 2 K /w in case ofw = 1?
Homework Equations
The crossover frequency wc is the frequency where the absolute value of the transfer function equals to one. It is also where the graph crosses the x-axis (frequency axis). Is this right?
The Attempt at a Solution
Last edited: