- #1
albertrichardf
- 165
- 11
Hi,
I read the Feynman Lectures Volume 1, Chapter 27, section 27-7, which can be here. In the lecture he describes the fundamental limits of resolution and provides a criterion.
Here is the diagram I am referring to, figure 27.-9:
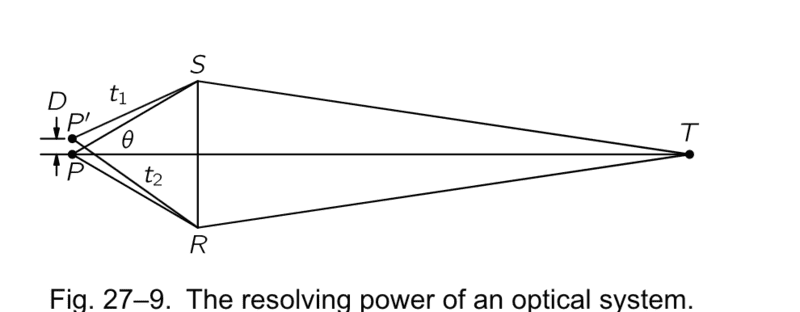
There are two light sources, ##P## and ##P'## There is an optical system, which is just a line ##SR## and it gets the light from sources ##P## and ##P'## to converge. Suppose that the image of ##P## is formed at ##T##, which is where the lines ##PST## and ##PRT## meet. Now draw the lines ##P'RT## and ##P'ST##. If the two points ##P## and ##P'## are to be resolved, Feynman gives the formula 27.17:
$$t_2 - t_1 < \frac {1}{\nu} $$
where ##t_2## and ##t_1## are the times for the paths ##P'RT## and ##P'ST##, respectively and ##\nu## is the frequency of the light.
He then goes on to state that this equation is exactly equivalent to the following:
$$ D = \frac {\lambda}{n sin (\theta)} $$
where ##D## is the distance ##PP'##, ##\lambda## is the wavelength of the light, ##n## is the refractive index of the light at point ##P## and ##\theta## is the opening angle of the lens at ##SR##.
I have tried to derive this equation, but I ended up with a factor of 2 in the denominator. That is, I got:
$$ D = \frac {\lambda}{2n sin (\theta)} $$
To get that I dropped perpendiculars between ##P'S## and ##PS##, and ##P'R## and ##PR##. Then I calculated the difference in distances and summed the differences. The sum of the differences gives me ##P'R - P'S##, since ##PR = PS##. Then I end up with:
$$ P'R - P'S = 2 D sin\theta $$
I then multiplied throughout by ##\frac nc ## to get the times on the left hand side. Then I used the inequality that was given to obtain the result I did.
What did I do wrong in this derivation?
Thank you for answering.
I read the Feynman Lectures Volume 1, Chapter 27, section 27-7, which can be here. In the lecture he describes the fundamental limits of resolution and provides a criterion.
Here is the diagram I am referring to, figure 27.-9:
There are two light sources, ##P## and ##P'## There is an optical system, which is just a line ##SR## and it gets the light from sources ##P## and ##P'## to converge. Suppose that the image of ##P## is formed at ##T##, which is where the lines ##PST## and ##PRT## meet. Now draw the lines ##P'RT## and ##P'ST##. If the two points ##P## and ##P'## are to be resolved, Feynman gives the formula 27.17:
$$t_2 - t_1 < \frac {1}{\nu} $$
where ##t_2## and ##t_1## are the times for the paths ##P'RT## and ##P'ST##, respectively and ##\nu## is the frequency of the light.
He then goes on to state that this equation is exactly equivalent to the following:
$$ D = \frac {\lambda}{n sin (\theta)} $$
where ##D## is the distance ##PP'##, ##\lambda## is the wavelength of the light, ##n## is the refractive index of the light at point ##P## and ##\theta## is the opening angle of the lens at ##SR##.
I have tried to derive this equation, but I ended up with a factor of 2 in the denominator. That is, I got:
$$ D = \frac {\lambda}{2n sin (\theta)} $$
To get that I dropped perpendiculars between ##P'S## and ##PS##, and ##P'R## and ##PR##. Then I calculated the difference in distances and summed the differences. The sum of the differences gives me ##P'R - P'S##, since ##PR = PS##. Then I end up with:
$$ P'R - P'S = 2 D sin\theta $$
I then multiplied throughout by ##\frac nc ## to get the times on the left hand side. Then I used the inequality that was given to obtain the result I did.
What did I do wrong in this derivation?
Thank you for answering.