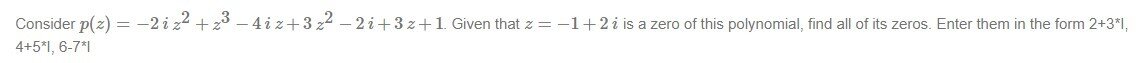- #1
TheFallen018
- 52
- 0
Hey, first off, I'm not sure if this is the right section. If another section is better, please let me know and I'll be more careful next time.
So, my problem is with a degree 3 complex polynomial. I'm given one zero of the equation, but since it is a complex zero, I can use the conjugate too. So, I already have two of the zeros for the polynomial, and since according to the fundamental theorem of algebra, it should only have one more. Because complex roots also have a conjugate, this suggests that the root is real. However, I'm having a hard time pinning it down. I've come up with a number of answers, and one of my more recent attempts led me to think it was -1. None of these seem right.
So, here's the question.
View attachment 8177
Any help would be amazing. Thank you :)
So, my problem is with a degree 3 complex polynomial. I'm given one zero of the equation, but since it is a complex zero, I can use the conjugate too. So, I already have two of the zeros for the polynomial, and since according to the fundamental theorem of algebra, it should only have one more. Because complex roots also have a conjugate, this suggests that the root is real. However, I'm having a hard time pinning it down. I've come up with a number of answers, and one of my more recent attempts led me to think it was -1. None of these seem right.
So, here's the question.
View attachment 8177
Any help would be amazing. Thank you :)