Centre of Mass of a Truncated Sphere

[Offside]

Alright... I've been struggling with this derivation for QUITE some time, and I can't get a hold of my TA... so...

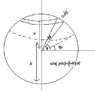
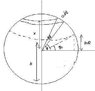
I'm trying to derive the centre of mass of a truncated sphere. The final answer is cm= -(3h^2*(R-h/2)^2)/(4R^3-3Rh^2+h^3) Where R is the radius of the full sphere, and h is the height of the truncation. I'm trying to use a double integral, using the symmetry of the sphere, but I eother can't get the limits of integration right, or something in my math is wrong...

I also have 2 other derivations to do in this lab that I'm struggling with... I'll throw them out too...

cm = (8*pi*R^2)/(5*g*T^2) - This one, I can't seem to find relations that put all of these variables together (a rough start, I know...)

And... The moment of inertia of the missing spherical cap.

I(sc) = 3/2(M(cap)/3R-h)*(4/3R^2*h-Rh^2+h^3/5). Here, I'm trying to use rings of radius "r" and relate them to R and the z-axis, but again... something's not working out at all. (I may have the wrong idea on this problem to begin with... if only I lived close to my school... *sigh*)

I know this is a lot, but ANY help would be appreciated... even just a gentle push in the right direction for any of them...

Thanks!

 

[Gamma]

cm= -(3h^2*(R-h/2)^2)/(4R^3-3Rh^2+h^3)

Are you sure there are no any typo? I have got the following for cm.

cm= -\frac{3h^2*(R-h/2)^2}{2R^3-3Rh^2+h^3}

In the denominator, 2R^3 instead of 4R^3.

 

[Offside]

Sadly, I'm sure of the formula... or at least, that's what's given to me. Maybe it's a typo on the page, or you missed a factor of 2...

I'm going to keep plugging at it... I left it alone for the evening hoping to have a new perspective on it, but it doesn't seem to be helping. Don't suppose you could lend a hand as to how you made it where you did? Then I can at least check your answer... I know that's a little against the spirit of the site, but I'm starting to pull my hair out here...

I'll E-mail my TA about the 4 vs. 2 argument.

Thanks for the reply!

 

[Gamma]

\int x dm = \overline{x} \int dm

dm = \pi (R cos\theta)^2 (R d\theta cos \theta)\rho

dm = \pi R^3 \rho* cos^3\theta d\theta

x = R sin theta




R \int_a^b cos^3 \theta sin \theta d \theta = \overline{x} \int_a^b cos^3 \theta d \theta


Where sin \phi =\frac{h-R}{R}, a = \phi, b = \pi/2

 

[Offside]

I've been in classes all day... sorry for the lateness of my reply...

The final integral you left there... I did it, and got:

R(1/4(cos(phi))^4) = x_(2/3 - 1/3cos(phi)^2*((h-R)/R))

Now, I can't make out much on your diagram, but I'm pretty sure I can't find a way to get that into the correct form... I can't figure out how you would define cos(phi) from your diagram. Perhaps that's what I'm missing...

It's a different approach than I too, that's for sure. Significantly less math... I likes

Thanks in advance for the clarification.

 

[Gamma]

check your integral of

\int cos^3 \theta d \theta



About the diagram:

Sphere is truncated at the dotted line. The potion below the dotted line is gone. To find the cm of the remaining part, I have chosen a small element (disc) at angle theta.

Mass of the element, dm = area of the disc * thickness * mass density

Did you understand how I got the area and thickness?

Next you need to know the limits of the integral. We are integrating over theta. Range of theta starts at the dotted line and end at the top of the sphere. What is theta at dotted line? Let's say it is \phi. See the right triangle. Can you figure out what is sin (phi)?

If you know sin phi, you can find cos phi.



At the top theta = pi/2

 

[Offside]

I do indeed understand how you got the area and thickness... and I hope to use a similar method when I try and find the Moment of Inertia of the missing part of the sphere.

As for the integral, I forgot a piece on the end... oops! The indefinite integral is 2/3*Sin(phi)+1/3cos^2(phi)*sin(phi)... I can get the rest from there.

If my reasoning is correct, cos(phi)^2 (Because it's easier to type than cos(phi) alone) = R^2-(h-R)^2/R^2 (Which I really should have been able to figure out earlier... you're right... simple trig... aparently my mind is fried)

I think that should do it... I just have to simplify the mess I have in front of me... hopefully it all works out! I sincerely appreaciate all the help, Gamma. Thanks again!

EDIT - I keep coming up with (3/4)*h^2/R+h

Other than trying to write out every labourious step, can you see anywhere where I've gone wrong?

 

[Gamma]

\int cos^3 \theta d \theta = sin \theta - \frac{sin^3 \theta}{3}


Go from here. You will get the answer that was given. I had made a minor mistake earlier in my math and now am getting what your handout said.


\overline{x}= -\frac{3h^2*(R-h/2)^2}{4R^3-3Rh^2+h^3}

Good luck and let me know


Edit:

For the integral of cos^3 \theta, I used the substitution u = sin \theta. Comes out easily.

 

[Offside]

x = 3/4*h^2*(h-2*R)^2/(R^2*(4*R-3*h+R*h^3-3*R*h^2+3*h*R))

There's a bunch of extra terms in the denominator of the fraction... everything else is right. I can't simplify it anymore though.

I've switched from trying to work everything out by hand to a program that simplifies for me... here's what I've input...

c:=(R^2-(h-R)^2)^(1/2)/R; (For Cosine)

z:=isolate(x*(2/3-(h-R)/R+((h-R/R)^3)/3)=(R/4)*c^4,x); (Which isolates the expression for x)

simplify(z); (And the result is the first line).

Can you see any errors in the code?

 

[Gamma]

I am not a fan of using programs for simple simplifications. With all the parentheses, there can be mistakes. In your expression for z, you need to enclose h-R in parenthesis. NOw you have it as h-R/R which your software must be taking as h - 1.

See, this is why we can't rely on software.

Regards,

 

[Offside]

(3/4)*h^2/R+h IS THE SAME AS -(3h^2*(R-h/2)^2)/(4R^3-3Rh^2+h^3)

I used my program (which I know you hate) to factor the denominator... turns out, it factors to (R+h)(R-h/2)^2, which cancels part of the top term.

This all could have been ended a couple posts ago... my apologies for dragging it out, and my thanks again Gamma for your help!

Now, onto the Moment of Inertia for the missing cap! (And hopefully finding expressions that will allow me to mash together that other form of the centre of mass)

Thank you once agan, Gamma!

 

[Gamma]

You are welcome.