- #1
cianfa72
- 1,847
- 204
- TL;DR Summary
- About clock synchronization for Langevin ring-riding observer
Hello,
reading the wiki entry for Langevin observers on rotating disk - Born_coordinates I'm struggling with the following quoted sentence: But as we see from Fig. 1, ideal clocks carried by these ring-riding observers cannot be synchronized.
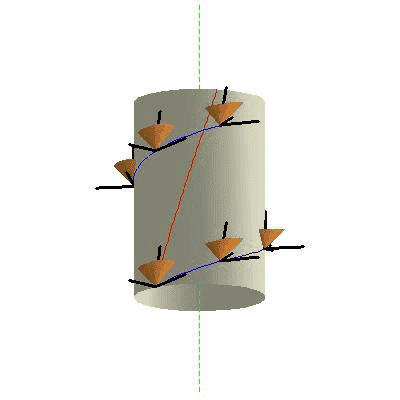
I do not grasp why, starting from the figure, those ring-riding clocks cannot be synchronized.
Thanks.
reading the wiki entry for Langevin observers on rotating disk - Born_coordinates I'm struggling with the following quoted sentence: But as we see from Fig. 1, ideal clocks carried by these ring-riding observers cannot be synchronized.
I do not grasp why, starting from the figure, those ring-riding clocks cannot be synchronized.
Thanks.