Continuity of f^+ .... Browder Corollary 3.13

[Math Amateur]

TL;DR Summary

I need help in order to demonstrate a formal and rigorous proof that given a real function f is continuous that $f^+$ is also continuous ... ...

I am reading Andrew Browder's book: "Mathematical Analysis: An Introduction" ... ...

I am currently reading Chapter 3: Continuous Functions on Intervals and am currently focused on Section 3.1 Limits and Continuity ... ...

I need some help with the proof of Corollary 3.13 ...Corollary 3.13 reads as follows:

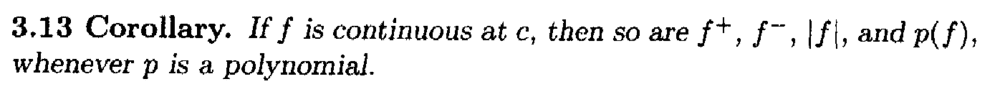Can someone help me to prove that if $f$ is continuous then $f^+ = \text{max} (f, 0)$ is continuous ...My thoughts are as follows:

If $c$ belongs to an interval where $f$ is positive then $f^+$ is continuous since $f$ is continuous ... further, if $c$ belongs to an interval where $f$ is negative then $f^+$ is continuous since $g(x) = 0$ is continuous ... but how do we construct a proof for those points where $f(x)$ crosses the $x$-axis ... ..
Help will be much appreciated ...

Peter

 

[fresh_42]

Hi Peter,

you got the right point where it might be a problem, namely when $f$ changes to $0$. Now a proof depends on the definition you use for a continuous function. You used "preimages of open sets are open" recently. So take an open set around such a point where $f$ crosses the $x-$axis and determine its preimage.

 

[member 587159]

A more general thing is true. If $f,g$ are continuous functions, then so is $f\lor g=\max\{f,g\}$.

The easiest way to see this is to note that

$$f\lor g=\frac{1}{2}(f+g+|f-g|)$$

 

[Math Amateur]

My thanks to Math_QED and fresh_42 for their help ...

Following the advice of fresh_42 my proof of the case where $f$ crosses the axis proceeds as follows:I think it will suffice to prove that $f^+$ is continuous for the case where a point $c_1 \in \mathbb{R}$ is such that for $x \lt c_1$, $f(x) = f^+(x)$ is positive and for $x \gt c_1$, $f^+(x) = 0$ ... ... while for some point $c_2 \gt c_1$ we have that $f^+(x) = 0$ for $x \lt c_2$ and $f(x) = f^+(x)$ is positive for $x \gt c_2$ ... ...

... see Figure 1 below ...

Now consider an (open) neighbourhood $V$ of $f^+(c_1)$ where...

$V= \{ f^+(x) \ : \ -f^+(a_1) \lt f^+(c_1) \lt f^+(a_1)$ for some $a_1 \in \mathbb{R} \}$

so ...

$V= \{ f^+(x) \ : \ -f^+(a_1) \lt 0 \lt f^+(a_1)$ for some $a_1 \in \mathbb{R} \}$ ...Then ... (see Figure 1) ...

$(f^+)^{ -1 } (V) = \{ a_1 \lt x \lt a_2 \}$ which is an open set as required ...

Further crossings of the x-axis by $f$ just lead to further sets of the nature $\{ a_{ n-1 } \lt x \lt a_n \}$ which are also open ... so ...

$(f^+)^{ -1 } (V) = \{ a_1 \lt x \lt a_2 \} \cup \{ a_3 \lt x \lt a_4 \} \cup \ldots \cup \{ a_{n-1} \lt x \lt a_n \}$

which being a union of open sets is also an open set ...The proof is similar if $f$ first crosses the x-axis from below ...
Is that correct?

Peter

 

[fresh_42]

You have written $f$, but we are interested in $f^+$. And the ordering is deliberate. Who guarantees you that $f(]x_1,x_2[)=]-y_1,y_1[$? What we want to know is, how the preimage of $(f^{+})^{-1}(]y_1,y_2[)$ looks like.

We start with an open interval $V\subseteq \mathbb{R}$. This is sufficient as any open set is a union of open intervals, and $(f^{+})^{-1}(\cup_\iota U_\iota) = \cup_\iota (f^{+})^{-1}(U_\iota)$ which is open if the individual sets are. Hence $V=]y_1,y_2[$. If $0\neq V$, then $f^+\equiv f$ or $f^+\equiv 0$ which are both continuous and we are done.

Thus we are left with $0\in V = ]y_1,y_2[$. What is $(f^{+})^{-1}(V)$ and how can we find out?

 

[Math Amateur]

You have written $f$, but we are interested in $f^+$. And the ordering is deliberate. Who guarantees you that $f(]x_1,x_2[)=]-y_1,y_1[$? What we want to know is, how the preimage of $(f^{+})^{-1}(]y_1,y_2[)$ looks like.

We start with an open interval $V\subseteq \mathbb{R}$. This is sufficient as any open set is a union of open intervals, and $(f^{+})^{-1}(\cup_\iota U_\iota) = \cup_\iota (f^{+})^{-1}(U_\iota)$ which is open if the individual sets are. Hence $V=]y_1,y_2[$. If $0\neq V$, then $f^+\equiv f$ or $f^+\equiv 0$ which are both continuous and we are done.

Thus we are left with $0\in V = ]y_1,y_2[$. What is $(f^{+})^{-1}(V)$ and how can we find out?

Oh ... that was a typo ... made a mistake copying my notes without thinking ... have edited it now ...

Is the post still in error ...?

... will now reflect on what you have written ...

Peter

 

[fresh_42]

I do not see where you get this very specific form of $V$ from. We have to show that $(f^+)^{-1}(V)$ is open for any open set $V\subseteq \mathbb{R}$. See my previous post for why we can assume that $V$ is an interval.

Now if $0\notin V$ then $(f^+)^{-1}(V)$ is either empty or $(f^+)^{-1}(V)=f^{-1}(V)$, which both are open sets. Thus we may assume that $0\in V$ and we have to determine $(f^+)^{-1}(V)$ for this case. Yes, $V$ looks like $V=(y_1,0)\cup \{0\} \cup (0,y_2)$ in this case, but we cannot know what $f^+$ does there, so we cannot write $y_1=f^+(a_1)\, , \,y_2=f^+(a_2)\,.$ Maybe $f^+(x)=f(x)> 1000$ and we have chosen $y_2=1$. The task is: Show that $(f^+)^{-1}((y_1,0)\cup \{0\} \cup (0,y_2))$ is open for any pair $y_1<0<y_2\,.$

If we want to consider continuity especially at $x=c$ where $f$ crosses the $x-$axis, then you should use the analytical $\varepsilon-\delta$ definition of continuity, not the topological. If you go by open sets, then any open set $V$ is possible.

You can still use @Math_QED 's approach which uses the theorem: certain combinations of continuous functions are again continuous.

 

[Math Amateur]

I do not see where you get this very specific form of $V$ from. We have to show that $(f^+)^{-1}(V)$ is open for any open set $V\subseteq \mathbb{R}$. See my previous post for why we can assume that $V$ is an interval.

Now if $0\notin V$ then $(f^+)^{-1}(V)$ is either empty or $(f^+)^{-1}(V)=f^{-1}(V)$, which both are open sets. Thus we may assume that $0\in V$ and we have to determine $(f^+)^{-1}(V)$ for this case. Yes, $V$ looks like $V=(y_1,0)\cup \{0\} \cup (0,y_2)$ in this case, but we cannot know what $f^+$ does there, so we cannot write $y_1=f^+(a_1)\, , \,y_2=f^+(a_2)\,.$ Maybe $f^+(x)=f(x)> 1000$ and we have chosen $y_2=1$. The task is: Show that $(f^+)^{-1}((y_1,0)\cup \{0\} \cup (0,y_2))$ is open for any pair $y_1<0<y_2\,.$

If we want to consider continuity especially at $x=c$ where $f$ crosses the $x-$axis, then you should use the analytical $\varepsilon-\delta$ definition of continuity, not the topological. If you go by open sets, then any open set $V$ is possible.

You can still use @Math_QED 's approach which uses the theorem: certain combinations of continuous functions are again continuous.

Hi fresh_42 ...

Thanks for your help ...

You write:

" ... ... I do not see where you get this very specific form of $V$ from. ... ... "

I'll try to explain ...

First, the context of my attempt at a proof was to show that $f^+$ was continuous at a point $c_1$ where $f$ crossed the x-axis from above ... that is the situation where point $c_1 \in \mathbb{R}$ is such that for $x \lt c_1$, $f(x) = f^+(x)$ is positive and for $x \geq c_1$, $f^+(x) = 0$ ... but I also considered f to be such that for some point $c_2 \gt c_1$ f crosses the x-axis from below ... ... that is for some point $c_2 \gt c_1$ we have that $f^+(x) = 0$ for $x \leq c_2$ and $f(x) = f^+(x)$ is positive for $x \gt c_2$ ... ...

The aim was to generalise from this specific form of $f$ and $f^+$ ... ...Now for this proof I am following Andrew Browder's book "Mathematical Analysis: An Introduction" ...

Browder defines a neighbourhood of a point $a \in \mathbb{R}$ as follows:

and I also followed Browder Proposition 3.9 (d) winch reads as follows:

So following Definition 3.3 and Proposition 3.9 I formed a neighbourhood $V$ of $f^+(c_1)$ as

$V= \{ f^+(x) \ : \ -f^+(a_1) \lt f^+(c_1) \lt f^+(a_1)$ for some $a_1 \in \mathbb{R} \}$

so ...

$V= \{ f^+(x) \ : \ -f^+(a_1) \lt 0 \lt f^+(a_1)$ for some $a_1 \in \mathbb{R} \}$ ...
I hope that makes sense...

Peter

 

[fresh_42]

Definition 3.3. defines a neighborhood and the subset topology. I wanted to use definition (d) (or (c)) of proposition 3.9. The crucial point is in both cases: for every neighborhood $V$. So we start with an arbitrary neighborhood of $0\in V$ since $f(c)=0$. We may assume $0\in V=(y_1,y_2)$. We may not assume $y_i=f^+(a_i)$ since this wouldn't be an arbitrary $V$.

Take your picture, rotate it by $90°$ to the left

and calculate $(f^+)^{-1}(V)$ for various possibilities of $f^+$.

 

[Math Amateur]

Definition 3.3. defines a neighborhood and the subset topology. I wanted to use definition (d) (or (c)) of proposition 3.9. The crucial point is in both cases: for every neighborhood $V$. So we start with an arbitrary neighborhood of $0\in V$ since $f(c)=0$. We may assume $0\in V=(y_1,y_2)$. We may not assume $y_i=f^+(a_i)$ since this wouldn't be an arbitrary $V$.

Take your picture, rotate it by $90°$ to the left
View attachment 255805
and calculate $(f^+)^{-1}(V)$ for various possibilities of $f^+$.

View attachment 255807

I have started to examine some possibilities for $f^+$ ... calculating $(f^+)^{-1} (V)$ for each ...

Examples are as follows:

For $f^+$ as shown in Figure 2 we have:

$V= \{ y \ : \ y_2 \lt y \lt y_1 \}$

so that

$(f^+)^{-1} (V) = \{ x \ : \ x_1 \lt x \lt x_2 \}$ ... ... ... ... ... which is an open set ...
For a second example consider $f^+$ as shown in Figure 3 below ... ...

For $f^+$ as shown in Figure 3 we have:

$V= \{ y \ : \ y_2 \lt y \lt y_1 \}$

so that

$(f^+)^{-1} (V) = \{ x \ : \ - \infty \lt x \lt x_2 \}$ ... ... ... ... ... which is an open set ...
For a third example consider $f^+$ as shown in Figure 4 below ... ...

For $f^+$ as shown in Figure 4 we have:

$V= \{ y \ : \ y_2 \lt y \lt y_1 \}$

so that

$(f^+)^{-1} (V) = \{ x \ : \ - \infty \lt x \lt x_1 \} \cup \{ x \ : \ x_2 \lt x \lt x_3 \}$ ... ... ... ... ... which is an open set ...
I have two questions ...

1. Is the above analysis correct as far as it goes ...?

2. If it is correct ... how do I use the analysis to organize and construct a general proof ... ...
Hope that you can help further ...

Peter

 

[fresh_42]

Yes, this looks ok so far. But listing all possibilities is a bit inconvenient.

We can assume that $f^+(\mathbb{R})\cap V \neq \emptyset$ since otherwise $(f^+)^{-1}(V)=\emptyset$ which is open and we are done. We can also assume that $f(c)= 0\in V$ for otherwise we have again $(f^+)^{-1}(V)=\emptyset$ or $(f^+)^{-1}(V)=f^{-1}(V)$ which is open by continuity of $f$.

Our $V$ looks like $V=(y_1,0) \cup \{0\} \cup (0,y_2)$ with $y_1<0<y_2$ so $(f^+)^{-1}(V)=(f^+)^{-1}((y_1,0))\cup (f^+)^{-1}(\{0\}) \cup (f^+)^{-1}((0,y_2)=\emptyset \cup (f^+)^{-1}([0,y_2))=(f^+)^{-1}([0,y_2))$.

Now we only have to bother, whether $y_2\in f(\mathbb{R})$ or not. So what is $(f^+)^{-1}([0,y_2))$ in these two cases?
a.) $y_2=f(x_2)$ for some $x_2\in \mathbb{R}$
b.) $y_2 > f(\mathbb{R})$

 

[Math Amateur]

Yes, this looks ok so far. But listing all possibilities is a bit inconvenient.

We can assume that $f^+(\mathbb{R})\cap V \neq \emptyset$ since otherwise $(f^+)^{-1}(V)=\emptyset$ which is open and we are done. We can also assume that $f(c)= 0\in V$ for otherwise we have again $(f^+)^{-1}(V)=\emptyset$ or $(f^+)^{-1}(V)=f^{-1}(V)$ which is open by continuity of $f$.

Our $V$ looks like $V=(y_1,0) \cup \{0\} \cup (0,y_2)$ with $y_1<0<y_2$ so $(f^+)^{-1}(V)=(f^+)^{-1}((y_1,0))\cup (f^+)^{-1}(\{0\}) \cup (f^+)^{-1}((0,y_2)=\emptyset \cup (f^+)^{-1}([0,y_2))=(f^+)^{-1}([0,y_2))$.

Now we only have to bother, whether $y_2\in f(\mathbb{R})$ or not. So what is $(f^+)^{-1}([0,y_2))$ in these two cases?
a.) $y_2=f(x_2)$ for some $x_2\in \mathbb{R}$
b.) $y_2 > f(\mathbb{R})$

Thanks again for your help, fresh_42 ...

You write:

" ... ...
So what is $(f^+)^{-1}([0,y_2))$ in these two cases?
a.) $y_2=f(x_2)$ for some $x_2\in \mathbb{R}$
b.) $y_2 > f(\mathbb{R})$ ... ... "Based on what was indicated by the examples I considered ...

... if $y_2=f(x)$ for some $x \in \mathbb{R}$

... then ...

$(f^+)^{-1} (V) = \{ x \ : \ x_1 \lt x \lt x_2 \} \cup \{ x \ : \ x_3 \lt x \lt x_4 \} \cup \ldots \cup \{ x \ : \ x_{n-1} \lt x \lt x_n \}$

where $x_1$ and/or $x_n$ may have to be replaced by $- \infty$ and $+ \infty$ respectively ... and the number of unions may be countably infinite ...

In all these cases $(f^+)^{-1} (V)$ is an open set ...

... ...

If $y_2 > f(\mathbb{R})$ ...

... then ...

$(f^+)^{-1} (V) = \emptyset$ ... ... and $\emptyset$ is an open set ...Is the above correct?

Peter*** EDIT ***

Correction to the following:

" ... ...

If $y_2 > f(\mathbb{R})$ ...

... then ...

$(f^+)^{-1} (V) = \emptyset$ ... ... and $\emptyset$ is an open set ... ... "It should read as follows:If $y_2 > f(\mathbb{R})$ ...

... then ...

$(f^+)^{-1} (V) = \mathbb{R}$ ... ... and $\mathbb{R}$ is an open set ...Hope that part of my answer is now correct ...

Also suspect that I was in error in not dealing with 0 properly in the expression $(f^+)^{-1}([0,y_2))$

Peter

 

[fresh_42]

No, it's not. Don't make it too complicated with the many subintervals. We do not need to and cannot know the details of $f$. What we need is $(f^+)^{-1}(V)=(f^+)^{-1}([0,y_2))$.

We also said that we may assume that f touches the $x-$axis, so we have either $(f^+)^{-1}([f^+(c),f^+(x)))$ or $(f^+)^{-1}([0,y_2))$ where $y_2> f^+(x)$ for all $x$.

Now forget for a moment the specific situation. Let's assume we have a function $g: \mathbb{R} \longrightarrow [0,\infty)$. What is $g^{-1}([g(0),g(x)))$ and what is $g^{-1}([0,C))$ where $\operatorname{im}(g)=g(\mathbb{R})\subseteq [0,C)$ since $C$ is bigger than any function value?

What are the pre-images in these cases? Solve it for $g$ and replace $g$ by $f^+$ afterwards.

 

[Math Amateur]

No, it's not. Don't make it too complicated with the many subintervals. We do not need to and cannot know the details of ff. What we need is (f+)−1(V)=(f+)−1([0,y2))(f+)−1(V)=(f+)−1([0,y2)).

We also said that we may assume that f touches the x−x−axis, so we have either (f+)−1([f+(c),f+(x)))(f+)−1([f+(c),f+(x))) or (f+)−1([0,y2))(f+)−1([0,y2)) where y2>f+(x)y2>f+(x) for all xx.

Now forget for a moment the specific situation. Let's assume we have a function g:R⟶[0,∞)g:R⟶[0,∞). What is g−1([g(0),g(x)))g−1([g(0),g(x))) and what is g−1([0,C))g−1([0,C)) where im(g)=g(R)⊆[0,C)im⁡(g)=g(R)⊆[0,C) since CC is bigger than any function value?

What are the pre-images in these cases? Solve it for gg and replace gg by f+f+ afterwards.

I will try to answer your question ...

" ... ... Let's assume we have a function g:R⟶[0,∞). What is g−1([g(0),g(x))) and what is g−1([0,C)) where im(g)=g(R)⊆[0,C) since C is bigger than any function value? ... ... "Consider g−1([g(0),g(x))) given g as follows:

We have g−1([g(0),g(x)))=[0,x) ... ...

But not quite sure why we are determining this pre-image ...

Now consider g−1([0,C)) where im(g)=g(R)⊆[0,C) since C is bigger than any function value ... where we are given g as in Figure 6 below

We find g−1([0,C))=R
Can you help further ...

Peter

 

[fresh_42]

$g^{-1}([g(0),x)) =\{\,u\in \mathbb{R}\,|\,0\leq g(u)< g(x)\,\} = \{\,u\in \mathbb{R}\,|\, g(u)< g(x)\,\}$

We need the definition of $f^+$ faster than I thought, sorry. I have been too concentrated on how to get rid of the boundary $g(0)$ on the left.

What we now have is $(f^+)^{-1}([(f^+)(0),x)) =\{\,u \in \mathbb{R}\,|\,(f^+)(u)<(f^+)(x)\,\}$ and the next step is $\{\,u \in \mathbb{R}\,|\,(f^+)(u)<(f^+)(x)\,\} = \{\,u \in \mathbb{R}\,|\,f(u)<f(x)\,\}=f^{-1}(\;(-\infty,f(x)\;)$ which is open because $f$ is continuous.

 

[Math Amateur]

$g^{-1}([g(0),x)) =\{\,u\in \mathbb{R}\,|\,0\leq g(u)< g(x)\,\} = \{\,u\in \mathbb{R}\,|\, g(u)< g(x)\,\}$

We need the definition of $f^+$ faster than I thought, sorry. I have been too concentrated on how to get rid of the boundary $g(0)$ on the left.

What we now have is $(f^+)^{-1}([(f^+)(0),x)) =\{\,u \in \mathbb{R}\,|\,(f^+)(u)<(f^+)(x)\,\}$ and the next step is $\{\,u \in \mathbb{R}\,|\,(f^+)(u)<(f^+)(x)\,\} = \{\,u \in \mathbb{R}\,|\,f(u)<f(x)\,\}=f^{-1}(\;(-\infty,f(x)\;)$ which is open because $f$ is continuous.

Hi fresh_42 ...

Sorry to be slow ... but what is $x$ in the expression $g^{-1}([g(0),x))$ ... ?

Further ... could you please explain why/how ...

$g^{-1}([g(0),x)) =\{\,u\in \mathbb{R}\,|\,0\leq g(u)< g(x)\,\} = \{\,u\in \mathbb{R}\,|\, g(u)< g(x)\,\}$

Again ... sorry if I am asking the obvious ...

*** EDIT *** ... oh! presumably its just the definition of pre-image ...?

Peter

 

[fresh_42]

$x$ was a very bad choice. It forced me to switch to $u$ as variable name. I made this mistake in post #13.
Better would have been the cases: $[0,y_2)$ with $(f^+)(c)=0, (f^+)(x_2)=y_2$ and $[0,C)$ with $f^+(x)<C \;\forall\,x\in \mathbb{R}$.

It was meant as a point $(x,y)=(x_2,y_2=g(x_2))$ with some given image point on the right.

Edit: $x_2$ has to be chosen as $x_2=\sup\{\,x\in \mathbb{R}\,|\,f(x)=y_2\,\}.$

 

[Math Amateur]

$x$ was a very bad choice. It forced me to switch to $u$ as variable name. I made this mistake in post #13.
Better would have been the cases: $[0,y_2)$ with $(f^+)(c)=0, (f^+)(x_2)=y_2$ and $[0,C)$ with $f^+(x)<C \;\forall\,x\in \mathbb{R}$.

It was meant as a point $(x,y)=(x_2,y_2=g(x_2))$ with some given image point on the right.

OK ... understand ...

Thanks once again for all your help ...

Peter

 

[Math Amateur]

Hi fresh_42 ...

I thought I'd just (for completeness) set out the proof of the continuity of $f^+$ in terms of the variables we were talking about early on ...

Consider Case 1: $y_2 = f^+ (x_2)$ for some $x_2 \in \mathbb{R}$ ... ...

See Figure 7 below ...

We have $y_2 = f^+ (x_2) = f(x_2)$ ... and ... $f^+(c) = f(c) = 0$ ...

We are required to calculate $(f^+)^{-1} ( [0, y_2) )$ ...

We have ...

$(f^+)^{-1} ( [0, y_2) ) = \{ x\ : \ 0 \leq f^+ (x) \lt f^+ (x_2) \}$

... so ... $(f^+)^{-1} ( [0, y_2) ) = \{ x\ : \ f^+ (x) \lt f^+ (x_2) \}$

... therefore ... $(f^+)^{-1} ( [0, y_2) ) = \{ x\ : \ f(x) \lt f(x_2) \}$

... and therefore ... $(f^+)^{-1} ( [0, y_2) ) = f^{-1}( ( - \infty , f(x_2) ) )$

... and $f^{-1}( ( - \infty , f(x_2) ) )$ is an open set since $f$ is continuous ...
Now consider Case 2 where $y_2 \gt f( \mathbb{R} )$ ... see Figure 8 below ...

In Case 2 we have $(f^+)^{-1} ( [0, y_2) ) = \mathbb{R}$ ...

... and $\mathbb{R}$ is an open set ...Hopefully the above is correct...

Peter