Contour Integrals: Working Check

[WWCY]

Homework Statement

Hi all, could someone help me run through my work for these 2 integrals and see if I'm in the right direction? I'm feeling rather unsure of my work.

1) Evaluate $\oint _\Gamma Z^*dz$ along an anticlockwise circle of radius R centered at z = 0

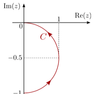
2) Calculate the contour integral $\int _C z^n dz$ where n ∈ N, and C is a semi-circle contour as shown:

Homework Equations

The Attempt at a Solution

1)
The contour is parameterized by $Z = Re^{i\theta}$, with $0 <\theta < 2\pi$. Therefore:

$\oint _\Gamma Z^*dz = \int_{\theta _ 1}^{\theta _2} d\theta \frac{dz}{d\theta} f(z(\theta))$ and,

$\int_{\theta _ 1}^{\theta _2} d\theta ( Rie^{i\theta}) (Re^{-i\theta})$ thus giving

$R^2i\int_{\theta _ 1}^{\theta _2} d\theta = 2\pi R^2 i$

2)

I define another integral $I' = \oint_\Gamma Z^n dz$ where $\Gamma$ forms a closed loop of the semi-circle with original contour C and an additional contour from 0i to -i that I define as C'

I then have,

$I' = \oint_\Gamma Z^n dz = \int_{C'} Z^n dz + \int_{C}Z^n dz$

According to Cauchy's integral theorem, $I'$ on the whole should give 0 as $Z^n$ is analytic everywhere in $\Gamma$, leaving me with

$- \int_{C'} Z^n dz = \int_{C}Z^n dz$

C' is parameterized by $Z = it$ with $t$ ranging from 0 to -1, hence

$- \int_{C'} Z^n dz = \int_{0}^{-1} dt \frac{dz}{dt} f(z(t))$

$- \int_{C'} Z^n dz = \int_{0}^{-1} dt(i)(it^n)$

$\int_{0}^{-1} dt(i)(it^n) = i^{n+1} \int_{0}^{-1} t^n dt = (i^{n+1})[\frac{-1^{n+1}}{n+1}]$

$\int_{C}Z^n dz = - \int_{C'} Z^n dz = (-1) (i^{n+1})[\frac{-1^{n+1}}{n+1}] = (i^{n+1})[\frac{-1^{n+2}}{n+1}]$

this then gives 2 solutions for odd and even $n$.

$\int_{C}Z^n dz = \frac{-i^{n+1}}{n+1}$ for odd $n$

$\int_{C}Z^n dz = \frac{i^{n+1}}{n+1}$ for even $n$

Help is greatly appreciated!

 

[Orodruin]

It looks mostly fine, but you really should not write $(-1)^k$ as $-1^k$. With correct order of operations, exponentiation comes before subtraction and so $-1^k = -1$.

Also, instead of writing your result as separate expressions for odd and even $n$, I suggest using that $-1 = i^{-2}$ in order to simplify your expression significantly.

 

[WWCY]

Also, instead of writing your result as separate expressions for odd and even $n$, I suggest using that $-1 = i^{-2}$ in order to simplify your expression significantly.

Hi @Orodruin, thanks for assisting, I will make the necessary adjustments.

With regards to the quote above, I realized that I could re-write the odd n solution as $\frac{i^{n-1}}{n+1}$, but I can't see how I can combine the answers as per the suggestion. Do you mind elaborating? Thank you!

 

[Orodruin]

Start with the general expression

$(i^{n+1})[\frac{(-1)^{n+2}}{n+1}]$

and use $-1 = i^{-2}$ instead of trying to start from the separated expressions.

 

[WWCY]

Start with the general expression

and use $-1 = i^{-2}$ instead of trying to start from the separated expressions.

This gives $\frac{i^{-(n+1)}}{n+1}$ for all n, is that right?

 

[Orodruin]

You should check your computation by checking if it holds for some particular $n$. Try it for $n = 0$.

 

[WWCY]

Whoops, made a ridiculous error. I believe it should've been $\frac{i^{-(n+3)}}{n+1}$ instead, is that right?

 

[Orodruin]

That is correct, although I would multiply it by $1 = i^4$ to get a slightly more aesthetically pleasing form (not having a 3 in there).

 

[WWCY]

That is correct, although I would multiply it by $1 = i^4$ to get a slightly more aesthetically pleasing form (not having a 3 in there).

Right, I'll do that as well! Thank you for your assistance and patience.