- #1
PainterGuy
- 940
- 69
Hi,
I was trying to derive relativistic momentum equation using classical momentum equation but it didn't work. Could you please help me? Thank you!
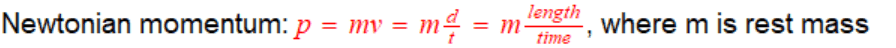


Where am I wrong? Or, is not possible, in any way, to derive relativistic momentum using Newtonian momentum equation? Thanks!
I was trying to derive relativistic momentum equation using classical momentum equation but it didn't work. Could you please help me? Thank you!
Where am I wrong? Or, is not possible, in any way, to derive relativistic momentum using Newtonian momentum equation? Thanks!
Last edited: