Demostration of the Uncertainty Principle from a given ket

[nikoladjal]

1. Homework Statement

I have to demonstrate the Uncertainty Principle

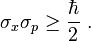
Starting from the expression of the following ket:

|Ψa>=(ax^+ibp^)|Ψ>

where a and b are complex numbers and the ^ denotes that x and p are unitary vectors.

2.Relevant equations

I must use the bra-ket notation, but I don't really have guidelines about the procedure to follow or the equations to use.3. The attempt at a solution

I thought about solving it trying to demostrate that <Ψa|Ψa> must be equal or greater to zero, but this implies integrate a expresion in two dimenssions of the phase space that I don't know how to solve. I though about using a projection operator, but all my tries went wrong, so I don't know if this is the right procedure.

Thank you for your help.

 

[BvU]

Hello Nikoladjal,

This is quite an involved exercise. You want to sort out what you have available to deal with it, and collect the relevant equations. A bit more than just "bra-ke notation". I'll give you a few to consider:

• The expectation value for any observable $A$
• The expression for $\sigma^2$ (being such an observable)
• The Schwarz inequality
• How your $\Psi_a$ fits in all of this

And then you want to embark on the solution phase; please show your steps. Just thinking and saying "can't do" does not count in PF . Getting stuck is no problem: that's what PF is for. But you can't get stuck if you don't take some steps first.

 

[nikoladjal]

Thank you BvU. Here is some information about the procedure I followed.

I used the condition for <Ψa|Ψa> having to be equal or greater than zero, and I solved the integral. I did the substitution of the operators x and p, and I have the following expression:

<Ψa|Ψa>= a^2<x^2>+b^2<p^2>+∫Ψ*[x,p]ΨdV

Where the terms between brackets <> define expected values and the term in [] is a commutator.

Someone knows if I can obtain the expression of the uncertainty principle with this, demonstrating that it has to be greater than zero?

 

[BvU]

How can you manipulate things so you end up with a $\sigma_x$ and a $\sigma_p$ (c.q. their product, or their product squared..) ?
All I see now is an $<x^2>$ and a $<p^2>$ (and an integral where a and b have mysteriously disappeared ).

 

[nikoladjal]

How can you manipulate things so you end up with a $\sigma_x$ and a $\sigma_p$ (c.q. their product, or their product squared..) ?
All I see now is an $<x^2>$ and a $<p^2>$ (and an integral where a and b have mysteriously disappeared ).

My fault, the a and b are there, I forgot to include them.

I'll put here the guideline I followed (I'm not sure it's right):

I began with this (where x and p are the operators position and momentum):

<Ψa|Ψa>= ∫Ψ*(ax-ibp)·Ψ(ax+ibp)dV = ∫Ψ*($a^2$·$x^2$+$b^2$·$p^2$+iab(xp-px))Ψ adV = ∫Ψ*($a^2$·$x^2$)ΨdV+
∫Ψ*($b^2$·$p^2$)ΨdV+iab∫Ψ*([x,p])ΨdV

And, the first two ones are the expressions of the expected values of the squared operators, so:

<Ψa|Ψa>= $a^2$·$<x^2>$+$b^2$·$<p^2>$+iab∫Ψ*([x,p])ΨdV

And that's the equation I must equal to zero to obtain de Uncertainty Principle. It's correct? In that case, some ideas of how can I follow, or any guidelines to do it another way if this is wrong?

Thank you for your time and the patience with a novice.

 

[BvU]

I'm not much better at the Heisenberg stuff than any novice (brought up with the Schroedinger picture) - which is why I'm following this with great interest (I'm learning too !).

I get the idea you forget $a$ and $b$ are complex numbers ?
Anyway, I see the $\hbar$ appearing from $[x,p] = i\hbar$, but what about the various $\sigma$ ?

And that's the equation I must equal to zero to obtain de Uncertainty Principle

Don't think so: what does that have to do with $\sigma_x \sigma_p$ ?

 

[nikoladjal]

I'm not much better at the Heisenberg stuff than any novice (brought up with the Schroedinger picture) - which is why I'm following this with great interest (I'm learning too !).

I get the idea you forget $a$ and $b$ are complex numbers ?
Anyway, I see the $\hbar$ appearing from $[x,p] = i\hbar$, but what about the various $\sigma$ ?

Don't think so: what does that have to do with $\sigma_x \sigma_p$ ?

Yes, a and b are complex, but I think that doesn't interferes with the calculus I made, no?

I can't see neither the correlation between σxσp and my result, but the tip they give to us is that it can be made with the condition <Ψa|Ψa>=>0. and that's the only expression I could reach for that. Maybe there's another way to get another result, but I didn't find it yet.

 

[BvU]

Think of an expression for $\sigma_x^2$. Idem $\sigma_p^2$. And their product (or the square root thereof).

 

[nikoladjal]

I think I' ve finally made it. In the space we are working in, we can take symmetry and identify <x>=<p>=0 because all the states have the same probability. With this, I minimised the inequality we discussed before in the value c=b/a and I introduced the result of this back in the inequality. With this, and seeing that the commutator of x and p is, as you said, -ih, I could reach the result of the Principle without any problem. I hope the reasoning is correct, at least it seems to be for me.

Next goal: learn to use LaTEX so my posts in the forum could be more legible haha

Thank you, again, for your help. With your responses you made me think about the problem and that's a good way of learning how to do it.