- #1
alyafey22
Gold Member
MHB
- 1,561
- 0
Prove the following :
$\displaystyle \psi(n)= -\gamma \,+\,\sum^{n-1}_{k=1}\frac{1}{k}$
ZaidAlyafey said:Prove the following :
$\displaystyle \psi(n)= -\gamma \,+\,\sum^{n-1}_{k=1}\frac{1}{k}$
chisigma said:In...
http://www.mathhelpboards.com/f15/difference-equation-tutorial-draft-part-i-426/
... it has been demonstrated that, if $\displaystyle \phi(*)$ is the 'digamma function', then is ...
$\displaystyle \phi(n)= - \gamma + \sum_{k=0}^{n-1} \frac{1}{1+k}$ (1)
The little 'discrepancy' is probably justified from the fact that the definition of digamma function is a little controversial...
Kind regards
$\chi$ $\sigma$
chisigma said:The little 'discrepancy' is probably justified from the fact that the definition of digamma function is a little controversial... $\chi$ $\sigma$
ZaidAlyafey said:Can you please elaborate on that ?
chisigma said:$\displaystyle \psi(x)= - \gamma + \sum_{k=1}^{n-1} \frac{1}{k}$ (3) $\displaystyle \phi(x) = - \gamma + \sum_{k=1}^{n} \frac{1}{k}$ (6)
chisigma said:I have to confess one 'phobia' of my: I don't like the function $\displaystyle \Gamma (x)$ because any time I meet it I have to do terrible efforts to decide if it is $\displaystyle \Gamma(n)= (n-1)!$ or $\displaystyle \Gamma(n)= (n+1)!$... that's why I prefer the factorial function ...
ZaidAlyafey said:I assumed you meant $\psi(n)$ and $\phi(n)$ , I know this is correct for all integers but let us try to find $\psi(1)$
From (3) it is \(\displaystyle -\gamma \) but from (6) it is \(\displaystyle -\gamma+1\)
so which is correct !
chisigma said:Your question is very useful because permits me to remark an important topic... from my definition of digammma function descends that for x = n is...
$\displaystyle \phi(n) = - \gamma + \sum_{k=0}^{n-1} \frac{1}{k+1}$ (1)
... so that...
$\displaystyle \psi(1) = \phi(0) = 1 - \gamma$ (2)
... which is correct. From the 'standard definition' reported on 'MonsterWolfram' descends that for x=n is...
$\displaystyle \psi(n)= - \gamma + \sum_{k=1}^{n-1} \frac{1}{k}$ (3)
... so that...
$\displaystyle \psi(1) = - \gamma + \sum_{k=1}^{0} \frac{1}{k} = \infty$ (4)
Gulp! (Tmi)... Kind regards $\chi$ $\sigma$
I like Serena said:Wait!
Wolfram says $\psi(1)=-\gamma + H_0 = -\gamma$.
See here.
A sum that has an upper bound below the lower bound is an empty sum.
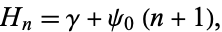
|
The Digamma function, denoted by ψ(x), is a special function that is the logarithmic derivative of the Gamma function. It is closely related to the Harmonic numbers, which are defined as the sum of the reciprocals of the positive integers up to a given number. Specifically, the Digamma function can be used to calculate the nth Harmonic number by taking the limit as x approaches infinity of ψ(x+1) - ψ(1).
The Digamma function and Harmonic numbers have numerous applications in mathematics, particularly in number theory, analysis, and combinatorics. They also have connections to other special functions and mathematical constants, such as the Euler-Mascheroni constant and the Riemann zeta function.
Yes, the Digamma function and Harmonic numbers can be extended to complex numbers. The complex Digamma function is a meromorphic function with simple poles at the non-positive integers. The complex Harmonic numbers are defined in a similar manner as their real counterparts, but with the summation extended to include all complex numbers.
The Digamma function and Harmonic numbers have applications in various fields, such as physics, engineering, and statistics. They are used in the calculation of sums, series, and integrals, as well as in the analysis of various systems and phenomena.
Yes, there are still many open problems and unsolved questions related to the Digamma function and Harmonic numbers. Some of these include finding closed forms for certain series involving Harmonic numbers, as well as studying the behavior of the Digamma function at certain points, such as rational and algebraic numbers.