Duncan G's Questions on Implicit Diff. & Related Rates

[MarkFL]

Here are the questions:

Related Rates and Implicit Differentiation Question? Please help!?

What is y'' (second derivative) of:
x^(1/2) + y^(1/2) = 1 ?

Find all points on the curve x^2*y^2 + x*y = 2 where the slope of the tangent line is -1.

At noon, ship A is 150 km west of ship B. Ship A is sailing east at 35 km/hr and ship is sailing north at 25 km/hr. How fast is the distance between the ships changing at 4:00 PM?

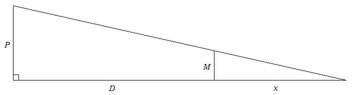
A street light is mounted at the top of a 15-ft-tall pole. A man 6 ft tall walks away from the pole with a speed of 5 ft/s along a straight path. How fast is the tip of his shadow moving when is 40 ft from the pole?

Thank you for your help.

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Duncan G,

1.) We are given the implicitly defined curve:

\(\displaystyle x^{\frac{1}{2}}+y^{\frac{1}{2}}=1\)

Implcitly differentiating with respect to $x$, we find:

\(\displaystyle \frac{1}{2}x^{-\frac{1}{2}}+\frac{1}{2}y^{-\frac{1}{2}}\frac{dy}{dx}=0\)

Solving for \(\displaystyle \frac{dy}{dx}\), we obtain:

\(\displaystyle \frac{dy}{dx}=-\frac{y^{\frac{1}{2}}}{x^{\frac{1}{2}}}\)

Implicitly differentiating again with respect to $x$, we get:

\(\displaystyle \frac{d}{dx}\left(\frac{dy}{dx} \right)=-\frac{x^{\frac{1}{2}}\frac{1}{2}y^{-\frac{1}{2}}\frac{dy}{dx}-y^{\frac{1}{2}}\frac{1}{2}x^{-\frac{1}{2}}}{\left(x^{\frac{1}{2}} \right)^2}\)

Using the first derivative, and simplifying, we get:

\(\displaystyle \frac{d^2y}{dx^2}=\frac{1+\frac{y^{\frac{1}{2}}}{x^{\frac{1}{2}}}}{2x}\)

Multiplying by \(\displaystyle \frac{x^{\frac{1}{2}}}{x^{\frac{1}{2}}}\), we have:

\(\displaystyle \frac{d^2y}{dx^2}=\frac{x^{\frac{1}{2}}+y^{\frac{1}{2}}}{2x^{\frac{3}{2}}}\)

Using the fact that \(\displaystyle x^{\frac{1}{2}}+y^{\frac{1}{2}}=1\), we then get:

\(\displaystyle \frac{d^2y}{dx^2}=\frac{1}{2x^{\frac{3}{2}}}\)

We can check this result by explicitly differentiating. Let's write the original relation as:

\(\displaystyle y=\left(1-x^{\frac{1}{2}} \right)^2\)

\(\displaystyle \frac{dy}{dx}=2\left(1-x^{\frac{1}{2}} \right)\left(-\frac{1}{2}x^{-\frac{1}{2}} \right)=1-x^{-\frac{1}{2}}\)

\(\displaystyle \frac{d^2y}{dx^2}=\frac{1}{2}x^{-\frac{3}{2}}=\frac{1}{2x^{\frac{3}{2}}}\)

2.) We are given the implicit relation:

\(\displaystyle x^2y^2+xy=2\)

and asked to find the points where the slope of the tangent line is $-1$. So, implcitly differentiating with respect to $x$, we find:

\(\displaystyle x^2\cdot2y\frac{dy}{dx}+2xy^2+x\frac{dy}{dx}+y=0\)

Moving all terms not having \(\displaystyle \frac{dy}{dx}\) as a factor to the right, we get:

\(\displaystyle x^2\cdot2y\frac{dy}{dx}+x\frac{dy}{dx}=-2xy^2-y\)

Factoring both sides:

\(\displaystyle \left(x(2xy+1) \right)\frac{dy}{dx}=-y(2xy+1)\)

Hence:

\(\displaystyle \frac{dy}{dx}=-\frac{y}{x}\)

Equating this slope to $-1$, we obtain:

\(\displaystyle y=x\)

Substituting for $y$ in the original equation, and writing in standard form, we may solve for $x$:

\(\displaystyle x^4+x^2-2=0\)

Factor:

\(\displaystyle \left(x^2+2 \right)\left(x^2-1 \right)=0\)

The first factor has imaginary roots, so we are left with:

\(\displaystyle x=\pm1\)

Now, since $y=x$, the two points are then:

\(\displaystyle (-1,-1),\,(1,1)\)

Here is a plot of the curve ant its two tangent lines with slope $-1$:

View attachment 1501

3.) Let's orient our coordinate axes such that ship A is at the origin at noon, and so ship B is at $(150,0)$. Thus, we may describe the position of each ship parametrically as follows:

Ship A:

\(\displaystyle x=35t\)

\(\displaystyle y=0\)

Ship B:

\(\displaystyle x=150\)

\(\displaystyle y=25t\)

If we let $D$ be the distance between the ships at time $t$, we may use the distance formula to write:

\(\displaystyle D^2(t)=(35t-150)^2+(25t)^2=50\left(37t^2-210t+450 \right)\)

Implicitly differentiating with respect to $t$, we find:

\(\displaystyle 2D(t)D'(t)=50(74t-210)=100(37t-105)\)

Hence:

\(\displaystyle D'(t)=\frac{50(37t-105)}{D(t)}=\frac{\sqrt{50}(37t-105)}{\sqrt{37t^2-210t+450}}\)

At 4:00 pm, we have $t=4$, and so we find:

\(\displaystyle D'(4)=\frac{\sqrt{50}(37(4)-105)}{\sqrt{37(4)^2-210(4)+450}}=\frac{215}{\sqrt{101}}\,\frac{\text{km}}{\text{hr}}\)

Thus, at 4:00 pm the distance between the ships is increasing at a rate of about 21.3933 kph.

4.) Please refer to the following diagram:

View attachment 1502

$P$ is the height of the pole, $M$ is the height of the man, $D$ is the man's distance from the pole, and $x$ is the length of the shadow.

By similarity, we find:

\(\displaystyle \frac{D+x}{P}=\frac{x}{M}\)

\(\displaystyle DM+Mx=Px\)

\(\displaystyle x=\frac{DM}{P-M}\)

Observing that $x$ and $D$ are changing with time, we find by implcitly differentiating with respect to time $t$, we have:

\(\displaystyle \frac{dx}{dt}=\frac{M}{P-M}\frac{dD}{dt}\)

Also observing that movement of the tip of the man's shadow is the result not only of the shadow growing but also of the man's movement, we find that we must add these rates of change, so that the rate of change of the point $T$ of the tip of the shadow is given by:

\(\displaystyle \frac{dT}{dt}=\frac{dD}{dt}+\frac{dx}{dt}=\frac{dD}{dt}\left(1+\frac{M}{P-M} \right)=\frac{P}{P-M}\frac{dD}{dt}\)

Now, using the given data (did you notice we do not need $D$?):

\(\displaystyle P=15\text{ ft},\,M=6\text{ ft},\,\frac{dD}{dt}=5\,\frac{\text{ft}}{\text{s}}\)

We find:

\(\displaystyle \frac{dT}{dt}=\frac{15}{15-6}\cdot5\,\frac{\text{ft}}{\text{s}}=\frac{25}{3}\,\frac{\text{ft}}{\text{s}}\)